Critical velocity and anaerobic paddling capacity determined by different mathematical models and number of predictive trials in canoe slalom

Abstract

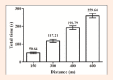
The purpose of this study was to analyze if different combinations of trials as well as mathematical models can modify the aerobic and anaerobic estimates from critical velocity protocol applied in canoe slalom. Fourteen male elite slalom kayakers from Brazilian canoe slalom team (K1) were evaluated. Athletes were submitted to four predictive trials of 150, 300, 450 and 600 meters in a lake and the time to complete each trial was recorded. Critical velocity (CV-aerobic parameter) and anaerobic paddling capacity (APC-anaerobic parameter) were obtained by three mathematical models (Linear1=distance-time; Linear 2=velocity-1/time and Non-Linear = time-velocity). Linear 1 was chosen for comparison of predictive trials combinations. Standard combination (SC) was considered as the four trials (150, 300, 450 and 600 m). High fits of regression were obtained from all mathematical models (range - R² = 0.96-1.00). Repeated measures ANOVA pointed out differences of all mathematical models for CV (p = 0.006) and APC (p = 0.016) as well as R² (p = 0.033). Estimates obtained from the first (1) and the fourth (4) predictive trials (150 m = lowest; and 600 m = highest, respectively) were similar and highly correlated (r=0.98 for CV and r = 0.96 for APC) with the SC. In summary, methodological aspects must be considered in critical velocity application in canoe slalom, since different combinations of trials as well as mathematical models resulted in different aerobic and anaerobic estimates. Key pointsGreat attention must be given for methodological concerns regarding critical velocity protocol applied on canoe slalom, since different estimates were obtained depending on the mathematical model and the predictive trials used.Linear 1 showed the best fits of regression. Furthermore, to the best of our knowledge and considering practical applications, this model is the easiest one to calculate the estimates from critical velocity protocol. Considering this, the abyss between science and practice may be decreased. Coaches of canoe slalom may simply apply critical velocity protocol and calculate by themselves the aerobic and anaerobic estimates.Still considering practical application, the results of this study showed the possibility of calculating the critical velocity estimates by using just two trials. These results are extremely relevant regarding saving time and easy applicability of this protocol for canoe slalom.

Keywords: Canoe slalom; aerobic parameter; anaerobic parameter; critical velocity; elite athletes; sports performance.

Figure 1.

a) Linear 1 model expressed between total distance covered (D) and time to covered the distance (T). b) Linear 2 model associated between velocity (V) and 1 divided by inverse of time (1/T). c) Non-Linear model corresponding by the relationship between total time to covered the distance (T) and velocity (V).

Figure 2.

Total times to complete the predictive trials of 150, 300, 450 and 600 meters.