Probabilistic inference in discrete spaces can be implemented into networks of LIF neurons
- PMID: 25729361
- PMCID: PMC4325917
- DOI: 10.3389/fncom.2015.00013
Probabilistic inference in discrete spaces can be implemented into networks of LIF neurons
Abstract
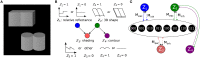
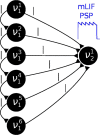
The means by which cortical neural networks are able to efficiently solve inference problems remains an open question in computational neuroscience. Recently, abstract models of Bayesian computation in neural circuits have been proposed, but they lack a mechanistic interpretation at the single-cell level. In this article, we describe a complete theoretical framework for building networks of leaky integrate-and-fire neurons that can sample from arbitrary probability distributions over binary random variables. We test our framework for a model inference task based on a psychophysical phenomenon (the Knill-Kersten optical illusion) and further assess its performance when applied to randomly generated distributions. As the local computations performed by the network strongly depend on the interaction between neurons, we compare several types of couplings mediated by either single synapses or interneuron chains. Due to its robustness to substrate imperfections such as parameter noise and background noise correlations, our model is particularly interesting for implementation on novel, neuro-inspired computing architectures, which can thereby serve as a fast, low-power substrate for solving real-world inference problems.
Keywords: Bayesian theory; MCMC; computational neural models; graphical models; neural coding; neuromorphic hardware; probabilistic models and methods; theoretical neuroscience.
Figures
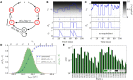
 (μ = 0, σ = 0.5). The green bars are the results of 10 simulations of duration 100 s. The error bars denote the standard error.
(μ = 0, σ = 0.5). The green bars are the results of 10 simulations of duration 100 s. The error bars denote the standard error.

References
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

