Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Jan-Feb;7(1):21-41.
doi: 10.1002/wics.1339.

Bayesian Models for fMRI Data Analysis

Linlin Zhang  1 , Michele Guindani  2 , Marina Vannucci  1
Affiliations

Bayesian Models for fMRI Data Analysis

Linlin Zhang et al. Wiley Interdiscip Rev Comput Stat. 2015 Jan-Feb.

Abstract

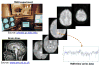
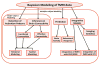
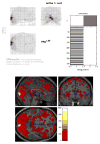
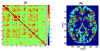
Functional magnetic resonance imaging (fMRI), a noninvasive neuroimaging method that provides an indirect measure of neuronal activity by detecting blood flow changes, has experienced an explosive growth in the past years. Statistical methods play a crucial role in understanding and analyzing fMRI data. Bayesian approaches, in particular, have shown great promise in applications. A remarkable feature of fully Bayesian approaches is that they allow a flexible modeling of spatial and temporal correlations in the data. This paper provides a review of the most relevant models developed in recent years. We divide methods according to the objective of the analysis. We start from spatio-temporal models for fMRI data that detect task-related activation patterns. We then address the very important problem of estimating brain connectivity. We also touch upon methods that focus on making predictions of an individual's brain activity or a clinical or behavioral response. We conclude with a discussion of recent integrative models that aim at combining fMRI data with other imaging modalities, such as EEG/MEG and DTI data, measured on the same subjects. We also briefly discuss the emerging field of imaging genetics.

Keywords: Bayesian Statistics; Brain Connectivity; Classification and Prediction; Spatio-Temporal Activation Models; fMRI.

PubMed Disclaimer

Figures

Figure 1
Figure 1
Typical fMRI experiment: 3D maps are acquired over time while the subject lies in the scanner, producing time series of fMRI BOLD responses measured at each brain voxel. Selected 2D arrays, corresponding to axial slices across the third dimension, are shown.
Figure 2
Figure 2
Outline of the Bayesian methods for fMRI data reviewed in this paper. Methods are divided according to the objective of the analysis.
Figure 3
Figure 3
Typical modeling of the BOLD signal at a given voxel, for both block and event-related designs. The BOLD signal is modeled as the convolution of the experimental stimulus and the hemodynamic response function (HRF).
Figure 4
Figure 4
Top left: An Example of PPMs generated with the software SPM8 (http://www.fil.ion.ucl.ac.uk/spm). Top right: Design matrix. Bottom: Overlay of χ2 statistic values showing regions where activity is different between active and rest conditions.
Figure 5
Figure 5
Functional connectivity. (a) Matrix of posterior estimates of inter-regional correlations (Bowman et al.); (b) Posterior clustering map of spatially remote voxels (Zhang et al. ).
Figure 6
Figure 6
Effective connectivity. Maximum a posteriori estimates of parameters measuring effective connectivity in an fMRI study on attention to motion (Stephan et al.).
Figure 7
Figure 7
Example of Diffusion Tensor Imaging (DTI) data.
See this image and copyright information in PMC

References

    1. Andersen AH, Gash DM, Avison MJ. Principal component analysis of the dynamic response measured by fMRI: a generalized linear systems framework. Magnetic Resonance Imaging. 1999;17(6):795–815. - PubMed
    1. Babajani-Feremi A, Bowyer S, Moran J, Elisevich K, Soltanian-Zadeh H. Variational Bayesian framework for estimating parameters of integrated E/MEG and fMRI model. SPIE Medical Imaging. 2009:72621T–72621T.
    1. Bhattacharya S, Maitra R. A nonstationary nonparametric Bayesian approach to dynamically modeling effective connectivity in functional magnetic resonance imaging experiments. The Annals of Applied Statistics. 2011;5(2B):1183–1206.
    1. Bhattacharya S, Ho M, Purkayastha S. A Bayesian approach to modeling dynamic effective connectivity with fMRI data. NeuroImage. 2006;30:794–812. - PubMed
    1. Bishop CM. Pattern Recognition and Machine Learning. Springer; 2006.

LinkOut - more resources