Hall and field-effect mobilities in few layered p-WSe₂ field-effect transistors

Abstract

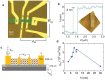
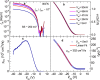
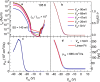
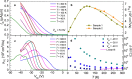
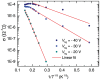
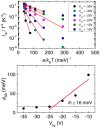
Here, we present a temperature (T) dependent comparison between field-effect and Hall mobilities in field-effect transistors based on few-layered WSe2 exfoliated onto SiO2. Without dielectric engineering and beyond a T-dependent threshold gate-voltage, we observe maximum hole mobilities approaching 350 cm(2)/Vs at T = 300 K. The hole Hall mobility reaches a maximum value of 650 cm(2)/Vs as T is lowered below ~150 K, indicating that insofar WSe2-based field-effect transistors (FETs) display the largest Hall mobilities among the transition metal dichalcogenides. The gate capacitance, as extracted from the Hall-effect, reveals the presence of spurious charges in the channel, while the two-terminal sheet resistivity displays two-dimensional variable-range hopping behavior, indicating carrier localization induced by disorder at the interface between WSe2 and SiO2. We argue that improvements in the fabrication protocols as, for example, the use of a substrate free of dangling bonds are likely to produce WSe2-based FETs displaying higher room temperature mobilities, i.e. approaching those of p-doped Si, which would make it a suitable candidate for high performance opto-electronics.

Figure 1

(a) Micrograph of the one of our WSe₂ field-effect transistors on a 270 nm thick SiO₂ layer on p-doped Si. Contacts, (Ti/Au) used to inject the electrical current (I_ds), are indicated through labels I⁺ (source) and I⁻ (drain), while the resistivity of the device ρ_xx was measured through either the pair of voltage contacts labeled as 1 and 2 or pair 3 and 4. The Hall resistance R_xy was measured with an AC excitation either through the pair of contacts 1 and 3 or 2 and 4. Length l of the channel, or the separation between the current contacts, is l = 15.8 μm while the width of the channel is w = 7.7 μm. (b) Height profile (along the blue line shown in the inset) indicating a thickness of 80 Å, or approximately 12 atomic layers for the crystal in (a). Inset: atomic force microscopy image collected from a lateral edge of the WSe₂ crystal in (a). (c) Side view sketch of our field-effect transistor(s), indicating that the Ti/Au pads contact all atomic layers, and of the experimental configuration of measurements. (d) Room temperature field-effect mobility μ_FE as a function of crystal thickness extracted from several FETs based on WSe₂ exfoliated onto SiO₂. The maximum mobility is observed for ~12 atomic layers.

Figure 2

(a) Current I_ds in a logarithmic scale as extracted from a WSe₂ FET at T = 300 K and as a function of the gate voltage V_bg for several values of the voltage V_ds, i.e. respectively 5 (dark blue line), 26 (red), 47 (blue), 68 (magenta), and 90 mV (brown), between drain and source contacts. Notice that the ON/OFF ratio approaches 10⁶ and subthreshold swing SS ~250 mV per decade. We evaluated the resistance R_c of the contacts by performing also 4 terminal measurements (see Fig. 7 a below) through R_c = V_ds/I_ds – ρ_xx l/w, where ρ_xx is the sheet resistivity of the channel measured in a four-terminal configuration. We found the ratio R_c/ρ_xx ≈ 20 to remain nearly constant as a function of V_bg. (b) Conductivity σ = S l/w, where the conductance S = I_ds/V_ds (from (a)), as a function of V_bg and for several values of V_ds. Notice, how all the curves collapse on a single curve, indicating linear dependence on V_ds. As argued below, this linear dependence most likely results from thermionic emission across the Schottky-barrier at the level of the contacts. (c) Field effect mobility μ_FE = (1/c_g dσ/dV_bg as a function of V_bg, where c_g = ε_rε₀/d = 12.789 × 10⁻⁹ F/cm² (for a d = 270 nm thick SiO₂ layer). (d) I_ds as a function of V_bg, when using an excitation voltage V_ds = 5 mV. Red line is a linear fit whose slope yields a field-effect mobility μ_FE ≈ 300 cm²/Vs.

Figure 3

(a) Current I_ds in a logarithmic scale as extracted from the same WSe₂ FET in Fig. 2 at T = 105 K and as a function of the gate voltage V_bg for several values of the voltage V_ds, i.e. respectively 5 (dark blue line), 26 (red), 47 (magenta), 68 (dark yellow), and 90 mV (brown). Notice that the ON/OFF ratio still approaches 10⁶. (b) Conductivity σ as a function of V_bg for several values of V_ds. Notice that even at lower Ts all the curves collapse on a single curve. Notice how the threshold gate voltage V^t_bg for conduction increases from ~0 V at 300 K to ~15 V at 105 K. Below, we argue that the observation of, and the increase of V^t_bg as T is lowered, corresponds to evidence for charge localization within the channel. (c) Field effect mobility μ_FE = (1/c_g) dσ/dV_bg as a function of V_bg. (d) I_ds as a function of V_bg, when using an excitation voltage V_ds = 5 mV. Red line is a linear fit whose slope yields a field-effect mobility μ_FE ≈ 665 cm²/Vs.

Figure 4

(a) I_ds as a function of the gate voltage V_bg for several temperatures T and for an excitation voltage V_ds = 5 mV. From the slopes of the linear fit (red line) one extracts the respective values of the field-effect mobility μ_FE as a function of the temperature, shown in (b). Orange markers depicts μ_FE for a second, annealed sample. The field-effect mobility is seen to increase continuously as the temperature is lowered down to T = 105 K, beyond which it decreases sharply. (c) μ_FE = (1/c_g) dσ/dV_bg as extracted from the curves in (a). Notice that μ_FE still saturates at a value of ≈ 300 cm²/Vs at T = 5 K. d Resistivity ρ = 1/σ as a function of T for 3 values of the gate voltage, i.e. −20, −30 and −40 V, respectively (as extracted from the data in (a) or (c)). Magenta line corresponds to a linear fit, describing the behavior of the metallic resistivity, defined by ∂ρ/∂T > 0, observed at higher temperatures when V_bg = −40 V.

Figure 5

Conductivity, i.e. σ = 1/ρ (from the data in Fig. 4 d, acquired under V_ds = 5 mV) in a logarithmic scale as a function of T^−1/3. Red lines are linear fits, indicating that at lower Ts and for gate voltages below a temperature dependent threshold value V^t_bg(T), σ(T) follows the dependence expected for two-dimensional variable-range hopping.

Figure 6

Top panel: Drain to source current I_ds as a function of (k_BT/e)⁻¹ for several values of the gate voltage V_bg (from the data in Fig. 4a). Red lines are linear fits from which we extract the value of the Schottky energy barrier ϕ_SB. Bottom panel: ϕ_SB in a logarithmic scale as a function of V_bg. Red line is a linear fit. The deviation from linearity indicates when the gate voltage matches the flat band condition from which we extract the size of the Schottky barrier Φ ≈ 16 meV.

Figure 7

(a) Four-terminal sheet resistance R_xx measured at a temperature of T = 300 K and as a function of V_bg for a second multilayered WSe₂ FET after annealing it under vacuum for 24 h. (b) Hall response R_xy = V_H(H)/I_ds as a function of the external magnetic field H, and for several values of the gate voltage V_bg. Red lines are linear fits from whose slope we extract the values of the Hall constant R_H( = V_H/HI_ds). (c) Density of carriers n_H = 1/(eR_H) induced by the back gate voltage as a function of V_bg. Red lines are linear fits from which, by comparing the resulting slope σ = n/V_bg = c_g*/e (c_g* is the effective gate capacitance). (d) Field-effect μ_FE (magenta and blue lines) and Hall μ_H = R_H/ρ_xx (red markers) mobilities (where ρ_xx = R_xxw/l, w and l are the width and the length of the channel, respectively) as functions of V_bg at T = 300 K. (e) Extracted Hall mobility μ_H as a function of T and for several values of V_bg. μ_H increases as T is lowered, but subsequently it is seen to decrease below a V_bg -dependent T. (f) Ratio between experimentally extracted and the ideal, or geometrical gate capacitances c_g*/c_g (black markers) and the mobilities μ_i = c_g*/c_g μ_H (V_bg = −60 V) (red markers) as functions of T. μ_i are the mobility values that one would obtain if the gate capacitance displayed its ideal c_g value in absence of spurious charges in the channel.