Forecast model analysis for the morbidity of tuberculosis in Xinjiang, China
- PMID: 25760345
- PMCID: PMC4356615
- DOI: 10.1371/journal.pone.0116832
Forecast model analysis for the morbidity of tuberculosis in Xinjiang, China
Abstract
Tuberculosis is a major global public health problem, which also affects economic and social development. China has the second largest burden of tuberculosis in the world. The tuberculosis morbidity in Xinjiang is much higher than the national situation; therefore, there is an urgent need for monitoring and predicting tuberculosis morbidity so as to make the control of tuberculosis more effective. Recently, the Box-Jenkins approach, specifically the autoregressive integrated moving average (ARIMA) model, is typically applied to predict the morbidity of infectious diseases; it can take into account changing trends, periodic changes, and random disturbances in time series. Autoregressive conditional heteroscedasticity (ARCH) models are the prevalent tools used to deal with time series heteroscedasticity. In this study, based on the data of the tuberculosis morbidity from January 2004 to June 2014 in Xinjiang, we establish the single ARIMA (1, 1, 2) (1, 1, 1)12 model and the combined ARIMA (1, 1, 2) (1, 1, 1)12-ARCH (1) model, which can be used to predict the tuberculosis morbidity successfully in Xinjiang. Comparative analyses show that the combined model is more effective. To the best of our knowledge, this is the first study to establish the ARIMA model and ARIMA-ARCH model for prediction and monitoring the monthly morbidity of tuberculosis in Xinjiang. Based on the results of this study, the ARIMA (1, 1, 2) (1, 1, 1)12-ARCH (1) model is suggested to give tuberculosis surveillance by providing estimates on tuberculosis morbidity trends in Xinjiang, China.
Conflict of interest statement
Figures


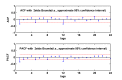
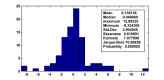
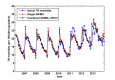

Similar articles
-
[Application of ARIMA model in predicting the incidence of tuberculosis in China from 2018 to 2019].Zhonghua Liu Xing Bing Xue Za Zhi. 2019 Jun 10;40(6):633-637. doi: 10.3760/cma.j.issn.0254-6450.2019.06.006. Zhonghua Liu Xing Bing Xue Za Zhi. 2019. PMID: 31238610 Chinese.
-
[Applications of multiple seasonal autoregressive integrated moving average (ARIMA) model on predictive incidence of tuberculosis].Zhonghua Yu Fang Yi Xue Za Zhi. 2007 Mar;41(2):118-21. Zhonghua Yu Fang Yi Xue Za Zhi. 2007. PMID: 17605238 Chinese.
-
Seasonality and Trend Forecasting of Tuberculosis Incidence in Chongqing, China.Interdiscip Sci. 2019 Mar;11(1):77-85. doi: 10.1007/s12539-019-00318-x. Epub 2019 Feb 8. Interdiscip Sci. 2019. PMID: 30734907
-
Application of an autoregressive integrated moving average model for predicting injury mortality in Xiamen, China.BMJ Open. 2015 Dec 9;5(12):e008491. doi: 10.1136/bmjopen-2015-008491. BMJ Open. 2015. PMID: 26656013 Free PMC article.
-
[Application of ARIMA model to predict number of malaria cases in China].Zhongguo Xue Xi Chong Bing Fang Zhi Za Zhi. 2017 Aug 15;29(4):436-440. doi: 10.16250/j.32.1374.2017088. Zhongguo Xue Xi Chong Bing Fang Zhi Za Zhi. 2017. PMID: 29508575 Chinese.
Cited by
-
Comparison of ARIMA, ETS, NNAR, TBATS and hybrid models to forecast the second wave of COVID-19 hospitalizations in Italy.Eur J Health Econ. 2022 Aug;23(6):917-940. doi: 10.1007/s10198-021-01347-4. Epub 2021 Aug 4. Eur J Health Econ. 2022. PMID: 34347175 Free PMC article.
-
Case report: multiple systemic disseminated tuberculosis mimicking lymphoma on 18F-FDG PET/CT.Medicine (Baltimore). 2017 Jul;96(29):e7248. doi: 10.1097/MD.0000000000007248. Medicine (Baltimore). 2017. PMID: 28723740 Free PMC article.
-
Using Autoregressive Integrated Moving Average (ARIMA) Modelling to Forecast Symptom Complexity in an Ambulatory Oncology Clinic: Harnessing Predictive Analytics and Patient-Reported Outcomes.Int J Environ Res Public Health. 2021 Aug 7;18(16):8365. doi: 10.3390/ijerph18168365. Int J Environ Res Public Health. 2021. PMID: 34444115 Free PMC article.
-
Development and comparison of predictive models for sexually transmitted diseases-AIDS, gonorrhea, and syphilis in China, 2011-2021.Front Public Health. 2022 Aug 12;10:966813. doi: 10.3389/fpubh.2022.966813. eCollection 2022. Front Public Health. 2022. PMID: 36091532 Free PMC article.
-
COVID-19 prevalence estimation: Four most affected African countries.Infect Dis Model. 2020;5:827-838. doi: 10.1016/j.idm.2020.10.002. Epub 2020 Oct 12. Infect Dis Model. 2020. PMID: 33073068 Free PMC article.
References
-
- Chinese Center for Disease Control and Prevention (2010) (The current situation of tuberculosis). Available: http://www.chinacdc.cn/jkzt/crb/jhb/jhb_3868/201003/t20100322_24566.htm. Accessed July 6th, 2014.
-
- Baidusection (2014) (Xinjiang Uygur Autonomous Region). Available: http://baike.baidu.com/subview/2824/14767092.htm?fr=aladdin#4_1. Accessed July 6th, 2014.
-
- Bureau of Health, Xinjiang Uyghur Autonomous Region (2014) (News release of the TB day in Xinjiang). Available: http://www.xjwst.gov.cn/zwgknry.jsp?urltype=news.NewsContentUrl&wbtreeid.... Accessed July 6th, 2014.
-
- Wang YJ, Zhao TQ, Wang P, Li SQ, Huang Z, et al. (2006) Applying linear regression statistical method to predict the epidemic of hemorrhagic fever with renal syndrome. Chinese Journal of Vector Biology and Control 17: 333–334.
-
- Bi P, Wu XK, Zhang FZ, Parton KA, Tong SL (1998) Seasonal rainfall variability, the incidence of hemorrhagic fever with renal syndrome, and prediction of the disease in low-lying areas of China. American Journal of Epidemiology 148: 276–281. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical

