FEM: feature-enhanced map
- PMID: 25760612
- PMCID: PMC4356370
- DOI: 10.1107/S1399004714028132
FEM: feature-enhanced map
Abstract
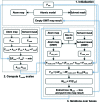
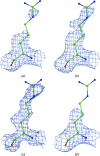
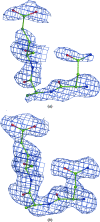
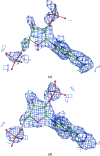
A method is presented that modifies a 2mFobs - DFmodel σA-weighted map such that the resulting map can strengthen a weak signal, if present, and can reduce model bias and noise. The method consists of first randomizing the starting map and filling in missing reflections using multiple methods. This is followed by restricting the map to regions with convincing density and the application of sharpening. The final map is then created by combining a series of histogram-equalized intermediate maps. In the test cases shown, the maps produced in this way are found to have increased interpretability and decreased model bias compared with the starting 2mFobs - DFmodel σA-weighted map.
Keywords: FEM; Fourier map; OMIT; PHENIX; cctbx; density modification; feature-enhanced map; map improvement; map kurtosis; map sharpening; model bias.
Figures











References
-
- Abramowitz, M. & Stegun, I. A. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, p. 928. New York: Dover.
-
- Adams, P. D. et al. (2010). Acta Cryst. D66, 213–221. - PubMed

