Estimating cellular parameters through optimization procedures: elementary principles and applications
- PMID: 25784880
- PMCID: PMC4347581
- DOI: 10.3389/fphys.2015.00060
Estimating cellular parameters through optimization procedures: elementary principles and applications
Abstract
Construction of quantitative models is a primary goal of quantitative biology, which aims to understand cellular and organismal phenomena in a quantitative manner. In this article, we introduce optimization procedures to search for parameters in a quantitative model that can reproduce experimental data. The aim of optimization is to minimize the sum of squared errors (SSE) in a prediction or to maximize likelihood. A (local) maximum of likelihood or (local) minimum of the SSE can efficiently be identified using gradient approaches. Addition of a stochastic process enables us to identify the global maximum/minimum without becoming trapped in local maxima/minima. Sampling approaches take advantage of increasing computational power to test numerous sets of parameters in order to determine the optimum set. By combining Bayesian inference with gradient or sampling approaches, we can estimate both the optimum parameters and the form of the likelihood function related to the parameters. Finally, we introduce four examples of research that utilize parameter optimization to obtain biological insights from quantified data: transcriptional regulation, bacterial chemotaxis, morphogenesis, and cell cycle regulation. With practical knowledge of parameter optimization, cell and developmental biologists can develop realistic models that reproduce their observations and thus, obtain mechanistic insights into phenomena of interest.
Keywords: likelihood; model selection; parameter optimization; probability density function; quantitative modeling.
Figures
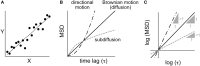
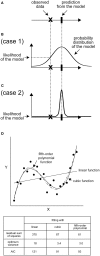
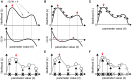
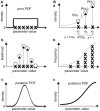
Similar articles
-
Speed and convergence properties of gradient algorithms for optimization of IMRT.Med Phys. 2004 May;31(5):1141-52. doi: 10.1118/1.1688214. Med Phys. 2004. PMID: 15191303
-
An improved hybrid of particle swarm optimization and the gravitational search algorithm to produce a kinetic parameter estimation of aspartate biochemical pathways.Biosystems. 2017 Dec;162:81-89. doi: 10.1016/j.biosystems.2017.09.013. Epub 2017 Sep 23. Biosystems. 2017. PMID: 28951204
-
Optimal Model Parameter Estimation from EEG Power Spectrum Features Observed during General Anesthesia.Neuroinformatics. 2018 Apr;16(2):231-251. doi: 10.1007/s12021-018-9369-x. Neuroinformatics. 2018. PMID: 29516302
-
Inference for Stochastic Chemical Kinetics Using Moment Equations and System Size Expansion.PLoS Comput Biol. 2016 Jul 22;12(7):e1005030. doi: 10.1371/journal.pcbi.1005030. eCollection 2016 Jul. PLoS Comput Biol. 2016. PMID: 27447730 Free PMC article.
-
How to deal with parameters for whole-cell modelling.J R Soc Interface. 2017 Aug;14(133):20170237. doi: 10.1098/rsif.2017.0237. Epub 2017 Aug 2. J R Soc Interface. 2017. PMID: 28768879 Free PMC article. Review.
Cited by
-
Systems biology: perspectives on multiscale modeling in research on endocrine-related cancers.Endocr Relat Cancer. 2019 Jun;26(6):R345-R368. doi: 10.1530/ERC-18-0309. Endocr Relat Cancer. 2019. PMID: 30965282 Free PMC article. Review.
-
Bayesian Inference of Forces Causing Cytoplasmic Streaming in Caenorhabditis elegans Embryos and Mouse Oocytes.PLoS One. 2016 Jul 29;11(7):e0159917. doi: 10.1371/journal.pone.0159917. eCollection 2016. PLoS One. 2016. PMID: 27472658 Free PMC article.
-
Inference of Internal Stress in a Cell Monolayer.Biophys J. 2016 Apr 12;110(7):1625-1635. doi: 10.1016/j.bpj.2016.03.002. Biophys J. 2016. PMID: 27074687 Free PMC article.
-
A Critical and Comparative Review of Fluorescent Tools for Live-Cell Imaging.Annu Rev Physiol. 2017 Feb 10;79:93-117. doi: 10.1146/annurev-physiol-022516-034055. Epub 2016 Nov 16. Annu Rev Physiol. 2017. PMID: 27860833 Free PMC article. Review.
-
Comprehensive Review of Models and Methods for Inferences in Bio-Chemical Reaction Networks.Front Genet. 2019 Jun 14;10:549. doi: 10.3389/fgene.2019.00549. eCollection 2019. Front Genet. 2019. PMID: 31258548 Free PMC article. Review.
References
-
- Akaike H. (1974). A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 10.1109/TAC.1974.1100705 - DOI
-
- Berg H. C. (1993). Random Walks in Biology. Princeton, NJ: Princeton University Press.
-
- Berg H. C. (2004). E. coli, in Motion, ed Berg H. C. (New York, NY: Springer Science and Business Media; ), 5–16.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

