Two-compartment passive frequency domain cochlea model allowing independent fluid coupling to the tectorial and basilar membranes

Abstract

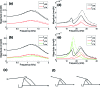
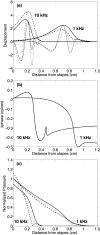
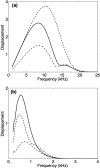
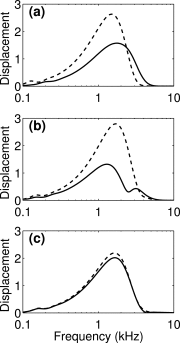
The cochlea is a spiral-shaped, liquid-filled organ in the inner ear that converts sound with high frequency selectivity over a wide pressure range to neurological signals that are eventually interpreted by the brain. The cochlear partition, consisting of the organ of Corti supported below by the basilar membrane and attached above to the tectorial membrane, plays a major role in the frequency analysis. In early fluid-structure interaction models of the cochlea, the mechanics of the cochlear partition were approximated by a series of single-degree-of-freedom systems representing the distributed stiffness and mass of the basilar membrane. Recent experiments suggest that the mechanical properties of the tectorial membrane may also be important for the cochlea frequency response and that separate waves may propagate along the basilar and tectorial membranes. Therefore, a two-dimensional two-compartment finite difference model of the cochlea was developed to investigate the independent coupling of the basilar and tectorial membranes to the surrounding liquid. Responses are presented for models using two- or three-degree-of-freedom stiffness, damping, and mass parameters derived from a physiologically based finite element model of the cochlear partition. Effects of changes in membrane and organ of Corti stiffnesses on the individual membrane responses are investigated.

FIG. 1.

Schematics of (a) the 2D fluid domain, showing the two compartments separated by the cochlear partition, (b) the cochlear partition, comprised of the organ of Corti, supported below by the BM and attached above to the TM, and (c) the cochlear partition model consisting of a series of two-degree-of-freedom systems positioned along the length of the cochlea. In the figures, the label “Scala vestibuli” refers to the combined scala vestibuli and scala media compartments.

FIG. 2.

Comparison of frequency response functions for detailed finite element model (solid line) and two- and three-degree-of-freedom approximations (dashed line). The frequency response functions shown are for forcing at the BM, but the other frequency response functions are similar. Frequency response functions at x = 10 mm for the (a) two-degree-of-freedom model and (b) three-degree-of-freedom model both match well the amplitudes and peak frequency of the finite element response. Frequency response functions at x = 2 mm have two peaks; the two-degree-of-freedom model results shown in (d) approximate the primary peak, while the three-degree-of-freedom model results shown in (e) are able to predict the double peak. Higher order models would produce an even better agreement, but would be more computationally expressive and less intuitive. Schematics of the deformed shape for forcing at the peak frequencies are given in (c) and (f), at x = 10 mm and x = 2 mm, respectively. The deformed shape corresponding to the higher frequency peak at x = 2 mm [right schematic of (f)] shows involvement of the second mode of the TM, suggesting that the TM may have a different effect on the cochlea response in the basal region.

FIG. 3.

Response of the two-degree-of-freedom model of the cochlear partition for 1 and 10 kHz excitation plotted versus distance from the stapes. (a) BM (solid line) and TM (dashed line) displacements (re stapes). (b) Phase difference between the BM and TM displacements. The BM and TM displacements are in phase at the stapes. The amplitude of the phase difference increases after the peak displacement until the TM leads the BM by approximately 1/2 cycle. (c) Normalized pressure amplitude at the BM (solid line) and TM (dashed line) surfaces. Half the pressure difference (dotted line) is shown for comparison to one compartment models. Pressures are normalized by half the pressure difference at the stapes. When the BM and TM displacements are significantly different, the pressures on the membranes also differ.

FIG. 4.

Transverse BM (solid line), transverse TM (dashed line), and tangential TM (dashed-dotted line) displacement amplitudes (re stapes) versus frequency for the three-degree-of-freedom model of the organ of Corti at (a) x = 2 mm, a basal position, and (b) x = 9 mm, an apical location.

FIG. 5.

Effect of the coupling strength between the TM and BM. Vertical (y direction) displacement amplitude (re stapes) of the BM (solid line) and TM (dashed line) at x = 6 mm versus frequency for the two-degree-of-freedom model of the cochlear partition for (a) k_OC = 0.04 k_BM, (b) k_OC = 0.4 k_BM, and (c) k_OC = 4 k_BM. For weak coupling, the traveling waves on the two membranes are uncoupled and have different frequency peaks. For intermediate coupling, the membrane interaction increases and interference can occur. For higher coupling, the membranes move together.

FIG. 6.

Effect of the relative membrane stiffnesses. Normalized difference in peak frequency as a function of $k_{\text{BM}}/k_{\text{TM}}$ for both a basal location at x = 2 mm (circles) and an apical location at x = 9 mm (squares). Results shown are for a coupling stiffness k_OC = 0.3 (k_BM + k_TM).

FIG. 7.

Effect of the TM stiffness gradient. Peak frequency of the BM (black line) and TM (gray line) versus position as the exponential slope of the TM stiffness is varied, with the TM stiffness at x = 6 mm held constant. All other material parameters are also held constant. The solid curve corresponds to $k_{\text{BM}}/k_{\text{TM}}=3$ and a coupling stiffness k_OC = 0.3 (k_BM + k_TM). Increasing the exponential slope of the TM stiffness by 10% (dashed line) and 20% (dotted line) has a greater effect on the average slope of the BM response, even though the BM properties are unchanged.