On disciplinary fragmentation and scientific progress

Abstract

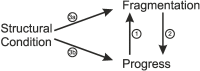
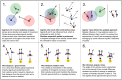
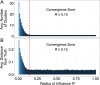
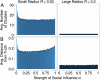
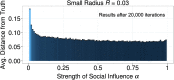
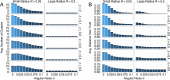
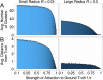
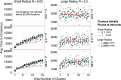
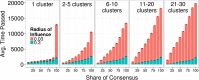
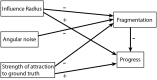
Why are some scientific disciplines, such as sociology and psychology, more fragmented into conflicting schools of thought than other fields, such as physics and biology? Furthermore, why does high fragmentation tend to coincide with limited scientific progress? We analyzed a formal model where scientists seek to identify the correct answer to a research question. Each scientist is influenced by three forces: (i) signals received from the correct answer to the question; (ii) peer influence; and (iii) noise. We observed the emergence of different macroscopic patterns of collective exploration, and studied how the three forces affect the degree to which disciplines fall apart into divergent fragments, or so-called "schools of thought". We conducted two simulation experiments where we tested (A) whether the three forces foster or hamper progress, and (B) whether disciplinary fragmentation causally affects scientific progress and vice versa. We found that fragmentation critically limits scientific progress. Strikingly, there is no effect in the opposite causal direction. What is more, our results shows that at the heart of the mechanisms driving scientific progress we find (i) social interactions, and (ii) peer disagreement. In fact, fragmentation is increased and progress limited if the simulated scientists are open to influence only by peers with very similar views, or when within-school diversity is lost. Finally, disciplines where the scientists received strong signals from the correct answer were less fragmented and experienced faster progress. We discuss model's implications for the design of social institutions fostering interdisciplinarity and participation in science.

Fig 1. Possible explanations for the correlation of scientific progress and fragmentation.

Each arrow represents one of the causal relationships that we study.

Fig 2. Ideal typical runs showing different patterns of consensus and level of scientific progress at four time steps: t = 1, 200, 1000, 2000.

Panel A shows a steady trend towards consensus ending up almost perfectly on the ground truth [R = 0.3, α = 0.5, τ = 0.9, σ = 0.01, ε = 0.1]. In Panel B, the same process of convergence ends up far away from truth [R = 0.3, α = 0.5, τ = 10, σ = 0.01, ε = 0.1]. Panel C shows the emergence of different schools of thought, that gradually merge together in proximity of the truth [R = 0.06, α = 0.9, τ = 3, σ = 0.02, ε = 0.25]. Panel D shows the emergence of many small clusters that persist over time[R = 0.03, α = 0.9, τ = 1, σ = 0.01, ε = 0.1]. Finally, in Panel E the process of school formation is so slow that even at the end of the simulation a relevant share of agents is still isolated [R = 0.03, α = 0.01, τ = 1, σ = 0.01, ε = 0.1].

Fig 3. Summary of model dynamics.

How the movement of agents in the epistemic space is affected by social influence (panels 2 and 3), attraction to ground truth (panel 4), and noise (panels 5 and 6).

Fig 4. (A) The effect of the influence radius R on the average number of clusters, and (B) the average distance from the ground truth at time point 2,000.

We identified a convergence zone (R > = 0.15) where dynamics always generated consensus in close proximity of the ground-truth. Error bars represent standard errors of the mean. [R = (0.01 − 1), α = 0.5, τ = 1, σ = 0.01, ε = 0.1]

Fig 5. (A) The effect of the strength of social influence α on the average number of clusters, and (B) the average distance from the ground truth at time point 2,000.

The effect of α is particularly strong for R = 0.03, and negligible for R = 0.3. In the case of a small radius of interaction, the U-shaped relationship depicted in Panel B is due to the high level of cohesiveness of the clusters at the beginning of the simulation, when social influence is very high. Error bars represent standard errors of the mean. [R = (0.03; 0.3), α = (0.01 − 0.99), τ = 1, σ = 0.01, ε = 0.1]

Fig 6. The effect of the strength of social influence α on the average distance from the ground truth at time point 20,000.

The U-shaped relationship depicted in Fig. 5 disappeared, and only low values of alpha cause a slower scientific progress. Error bars represent standard errors of the mean. [R = (0.03; 0.3), α = (0.01 − 0.99), τ = 1, σ = 0.01, ε = 0.1]

Fig 7. Average number of clusters (A), and average distance from ground-truth (B) for each combination of position noise (rows) and angular noise (x-axis within each row).

Angular noise is responsible for most of the variation of on both outcome measures, however higher values of position noise attenuate its effect. Error bars represent standard errors of the mean. [R = (0.03; 0.3), α = 0.5, τ = 1, σ = (0 − 0.05), ε = (0 − 0.5)]

Fig 8. The effect of the strength τ of attraction to ground truth on the average number of clusters (A), and the average distance from the ground truth (B) at time point 2,000.

In general, the weaker the attraction (higher values of τ) the more clusters the further away. However, most of the variation happens for values of τ between 1 and 20. Error bars represent standard errors of the mean. [R = (0.03; 0.3), α = 0.5, τ = (1 − 100), σ = 0.01, ε = 0.1]

Fig 9. Scatter plot clustering vs progress.

All data points are observations produced by Experiment 1.

Fig 10. The effects of fragmentation on progress.

At the beginning of the simulation agents were randomly preassigned to c = (1..15) clusters. Each group of agent was then placed at a fixed distance from the ground truth, and equidistant from the neighboring groups. We varied the distance between 0.2 and 1 in steps of 0.05 units for a small radius of interaction, and between 1.4892 and 2.2892 for a large radius of interaction. Graph shows the time necessary to 75% of the agents to end up in a radius of 0.05 units from truth. Simulations were stopped after 20,000 iterations. In general, a clustered field takes longer to build consensus, however the relationship is much more marked when interaction radius is small. On top of this, if also social influence is also weak, e.g. α = 0.01, reaching a consensus in proximity of the truth becomes virtually impossible. [R = (0.03, 0.3), α = (0.01, 0.5, 0.99), τ = 1, σ = 0.01, ε = 0.1]

Fig 11. Distributions of consensus shares X(10, .., 100) under different initial clustering conditions.

A field with a large radius of interaction can sustain a faster consensus growth for any intermediate share of consensus. Interestingly, if the interaction radius is small and agents are initially placed in a single cluster, it is extremely hard to reach full consensus (100% consensus share) due the to reduced social influence effects on those agents that manage to leave the initial cluster. Error bars represent standard errors of the mean. [R = (0.03, 0.3), α = (0.5, 0.99), τ = 1, σ = 0.01, ε = 0.1]

Fig 12. The effects of progress on fragmentation.

At the beginning of the simulation agents were randomly preassigned to c = (1..30) clusters. Each group of agent was then placed at a fixed distance from the ground truth, and equidistant from the neighboring groups. Panels A-D show results for a small radius R of interaction R = 0.03, and panels E-H for a large radius of interaction R = 0.3. We varied the initial distance from ground truth between 0.2 and 1 in steps of 0.05 units for a small radius of interaction, and between 1.4892 and 2.2892 for a large radius of interaction. We have then measured the number of clusters when a consensus share of 50% was reached. Results show that the average number of clusters is largely independent from the initial level of progress. In the case of a small radius, it is heavily determined by the initial number of clusters. Only in panel D (21 to 30 clusters), the first boxplot is lower than the rest because clusters are almost all connected at a distance of 0.2. [R = 0.03, α = (0.5, 0.99), τ = 1, σ = 0.01, ε = 0.1]

Fig 13. Effects that contribute to the correlation between fragmentation and progress.

Each arrow represents a significant causal relationships among those that we hypothesized in Fig. 1, according to the mediation analysis on the results of our formal model.