Continuous psychophysics: Target-tracking to measure visual sensitivity
- PMID: 25795437
- PMCID: PMC4371613
- DOI: 10.1167/15.3.14
Continuous psychophysics: Target-tracking to measure visual sensitivity
Abstract
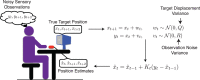
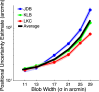
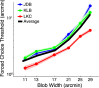
We introduce a novel framework for estimating visual sensitivity using a continuous target-tracking task in concert with a dynamic internal model of human visual performance. Observers used a mouse cursor to track the center of a two-dimensional Gaussian luminance blob as it moved in a random walk in a field of dynamic additive Gaussian luminance noise. To estimate visual sensitivity, we fit a Kalman filter model to the human tracking data under the assumption that humans behave as Bayesian ideal observers. Such observers optimally combine prior information with noisy observations to produce an estimate of target position at each time step. We found that estimates of human sensory noise obtained from the Kalman filter fit were highly correlated with traditional psychophysical measures of human sensitivity (R2 > 97%). Because each frame of the tracking task is effectively a "minitrial," this technique reduces the amount of time required to assess sensitivity compared with traditional psychophysics. Furthermore, because the task is fast, easy, and fun, it could be used to assess children, certain clinical patients, and other populations that may get impatient with traditional psychophysics. Importantly, the modeling framework provides estimates of decision variable variance that are directly comparable with those obtained from traditional psychophysics. Further, we show that easily computed summary statistics of the tracking data can also accurately predict relative sensitivity (i.e., traditional sensitivity to within a scale factor).
Keywords: Kalman filter; manual tracking; psychophysics; vision.
© 2015 ARVO.
Figures



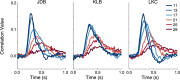


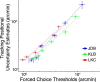
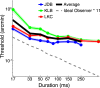
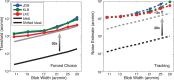
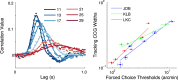
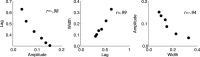
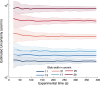
 ) versus experimental time used to estimate R. Error bounds show ±SEM. Blob width is indicated by curve color and identified in the legend by its σ in arcmin.
) versus experimental time used to estimate R. Error bounds show ±SEM. Blob width is indicated by curve color and identified in the legend by its σ in arcmin.References
-
- Ackermann J. F., Landy M. S. (2010). Suboptimal choice of saccade endpoint in search with unequal payoffs. Journal of Vision , 10 (7): 14, http://www.journalofvision.org/content/10/7/530, doi:10.1167/10.7.530. [Abstract] - DOI
-
- Brainard D. H. (1997). The psychophysics toolbox. Spatial Vision , 10, 433– 436. - PubMed
-
- Brett J. (1987). Goldilocks and the three bears (Retold and illustrated). New York: Dodd Mead.
-
- Brueggemann J. (2007). The hand is NOT quicker than the eye. Journal of Vision , 7 (15): 14, http://www.journalofvision.org/content/7/15/54, doi:10.1167/7.15.54. (Note: Actual authors were J. Brueggerman and S. Stevenson, but the latter was omitted from the published abstract by mistake.) - DOI
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

