The physics of proton therapy
- PMID: 25803097
- PMCID: PMC4407514
- DOI: 10.1088/0031-9155/60/8/R155
The physics of proton therapy
Abstract
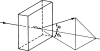
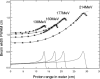
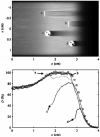
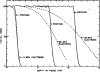
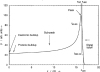
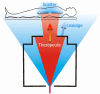
The physics of proton therapy has advanced considerably since it was proposed in 1946. Today analytical equations and numerical simulation methods are available to predict and characterize many aspects of proton therapy. This article reviews the basic aspects of the physics of proton therapy, including proton interaction mechanisms, proton transport calculations, the determination of dose from therapeutic and stray radiations, and shielding design. The article discusses underlying processes as well as selected practical experimental and theoretical methods. We conclude by briefly speculating on possible future areas of research of relevance to the physics of proton therapy.
Figures
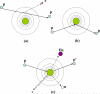
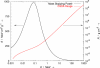
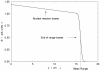
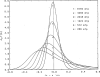













References
-
- AAPM . American Association of Physicists in Medicine Task Group 20: Protocol for heavy charged-particle therapy beam dosimetry. New York, NY: 1986.
-
- Agosteo S. Radiation protection constraints for use of proton and ion accelerators in medicine. Radiation Protection Dosimetry. 2009;137:167–86. - PubMed
-
- Agosteo S, Birattari C, Caravaggio M, Silari M, Tosi G. Secondary neutron and photon dose in proton therapy. Radiother Oncol. 1998;48:293–305. - PubMed
-
- Agostinelli S, Allison J, Amako K, Apostolakis J. Geant4 - A simulation toolkit. Nuclear Instruments and Methods A. 2003;506:250–303.
-
- Andreo P. On the clinical spatial resolution achievable with protons and heavier charged particle radiotherapy beams. Phys Med Biol. 2009;54:N205–15. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
