Fast Volume Reconstruction From Motion Corrupted Stacks of 2D Slices

Abstract

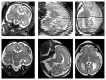
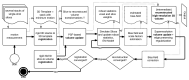
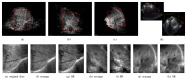
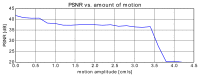
Capturing an enclosing volume of moving subjects and organs using fast individual image slice acquisition has shown promise in dealing with motion artefacts. Motion between slice acquisitions results in spatial inconsistencies that can be resolved by slice-to-volume reconstruction (SVR) methods to provide high quality 3D image data. Existing algorithms are, however, typically very slow, specialised to specific applications and rely on approximations, which impedes their potential clinical use. In this paper, we present a fast multi-GPU accelerated framework for slice-to-volume reconstruction. It is based on optimised 2D/3D registration, super-resolution with automatic outlier rejection and an additional (optional) intensity bias correction. We introduce a novel and fully automatic procedure for selecting the image stack with least motion to serve as an initial registration target. We evaluate the proposed method using artificial motion corrupted phantom data as well as clinical data, including tracked freehand ultrasound of the liver and fetal Magnetic Resonance Imaging. We achieve speed-up factors greater than 30 compared to a single CPU system and greater than 10 compared to currently available state-of-the-art multi-core CPU methods. We ensure high reconstruction accuracy by exact computation of the point-spread function for every input data point, which has not previously been possible due to computational limitations. Our framework and its implementation is scalable for available computational infrastructures and tests show a speed-up factor of 1.70 for each additional GPU. This paves the way for the online application of image based reconstruction methods during clinical examinations. The source code for the proposed approach is publicly available.

Fig. 1

Top row: An example of three orthogonal views through a stack of 3T ssFSE MRI slices. Note the significant motion artefacts between the slices and the intensity bias. The left image shows an acquired ssFSE slice and the other two images orthogonal planes through a stack of these slices. Bottom row: The resulting reconstruction at 0.75mm isotropic voxel size after applying the proposed method.

Fig. 2

An overview of the proposed approach. Thick solid lines represent the program flow and thin dotted lines the most important data flow. Boxes in dotted lines are optional, e.g., bias field correction for MR data.

Fig. 3

2D slices I_k are arranged in a volumetric 3D computation grid to maximize SIMD occupancy (left). The grid spans the maximum slice size in x and y. Smaller slices are filled with zeros to reach the required grid size in x and y. Operations on the reconstruction volume are performed in a volume X sized grid.

Fig. 4

Results of the application of our method to three stacks of freehand 2D compound ultrasound (US). This dataset is reconstructed to 0.6 mm isotropic voxel size and contains 568×406×630 voxels. The investigated area in red shows the vessel tree of a volunteer’s liver. (a-c) show a multi-planar reconstruction of the compounded average [3] of the input slices resampled in a joint volume with 0.6 mm isotropic voxel size. (d) gives an overview over two of the acquired 2D sweeps in 3D. (e) shows the original data, (f-k) show the resulting reconstruction in three orthogonal orientations comparing the average of the image data to the result of our super-resolution (SR) framework.

Fig. 5

Examples of a typical real motion corrupted scan (a) and a synthetically motion corrupted reconstructed dataset (b). Note that the slices shown serve only as illustration for the motion corruption artefacts and are not meant to show the same slices and same corruption in the same subject.

Fig. 6

Decreasing PSNR with artificially and randomly increasing motion tested on a real brain dataset. For this test we kept the number of iterations constant and used 4 stacks as proposed by Tuner.

Fig. 7

Comparison of the surrogate motion estimates (Eq. 3) and the amplitude actually used to simulate motion artefacts in a phantom dataset. The blue line shows the given, increasing motion amplitude and the connected dots show the result from our motion measurement approach.

Fig. 8

Comparison of different types of point spread functions for a 0.75mm voxel size reconstructed volume. (a) shows a slice through a reconstruction of a truncated and interpolated Gaussian weighted PSF_trunc [5], (b) using an accurately sampled Gaussian weighted PSF_Gauss (Eq. 6), (c) an accurately sampled Sinc/Gauss PSF_MRI (Eq. 7). (d) compared the intensity profile of the three PSFs at the line in (a-c). More distinct edges and finer details are provided by example (c).

Fig. 9

Comparison between an originally acquired slice (a) and cutting planes through the reconstructed volume at the same position. The reconstructions (b), (d), and (e) have the same resolution as the input (1.18mm voxel size) and use different point spread functions. Two rows in the images are selected (marked as white lines) and their intensity profiles are compared in (c) and (f). Note that using an accurately sampled PSF_MRI allows improved recovery of smaller details like the pupil in the eye (e). The PSF_MRI profiles are also closest to the originally measured slice profiles (blue vs. black curves).

Fig. 10

Qualitative comparison between BTK, KM, and the proposed approach: a fetal thoracic MR reconstruction (axial) and a reconstruction of the fetal brain (coronal), both acquired with a field strength of 3 Tesla. BTK’s minimum voxel size is defined by the minimum pixel size of the input stacks, which has been fixed for all tests (1.18 mm isotropic). The brain dataset shows a significant amount of motion and a 3T specific bias field, which causes a low reconstruction quality using BTK (d). The images show the same physical slices in world coordinates.