Hedging your bets: intermediate movements as optimal behavior in the context of an incomplete decision

Abstract

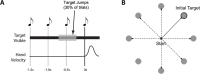
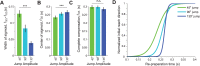
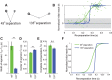
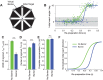
Existing theories of movement planning suggest that it takes time to select and prepare the actions required to achieve a given goal. These theories often appeal to circumstances where planning apparently goes awry. For instance, if reaction times are forced to be very low, movement trajectories are often directed between two potential targets. These intermediate movements are generally interpreted as errors of movement planning, arising either from planning being incomplete or from parallel movement plans interfering with one another. Here we present an alternative view: that intermediate movements reflect uncertainty about movement goals. We show how intermediate movements are predicted by an optimal feedback control model that incorporates an ongoing decision about movement goals. According to this view, intermediate movements reflect an exploitation of compatibility between goals. Consequently, reducing the compatibility between goals should reduce the incidence of intermediate movements. In human subjects, we varied the compatibility between potential movement goals in two distinct ways: by varying the spatial separation between targets and by introducing a virtual barrier constraining trajectories to the target and penalizing intermediate movements. In both cases we found that decreasing goal compatibility led to a decreasing incidence of intermediate movements. Our results and theory suggest a more integrated view of decision-making and movement planning in which the primary bottleneck to generating a movement is deciding upon task goals. Determining how to move to achieve a given goal is rapid and automatic.

Fig 1. Experiment 1 setup.

A) Subjects were trained to initiate movement synchronous with the last of four tones played at 500ms intervals. B) Subjects made center-out movements to “shoot” through one of 8 equally spaced targets. The target appeared synchronously with the first tone. On 30% of trials, the target was jumped by ±45°, ±90° or ±135° at a random time between 150 and 550ms before the fourth (i.e. final) tone. Solid arrow/bold target indicates movement required before target jump. Dashed arrows indicate potential movements required after a target jump.

Fig 2. Behavior of a representative subject in Experiment 1.

Left axes show the relationship between available re-preparation time (equal to the delay between target jump time and movement onset) and initial reach direction for 45° (A), 90° (C) and 135° (E) jumps. Each point represents a single jump trial. Solid lines indicate sigmoidal fits obtained by maximum likelihood estimation (see Methods). Shaded region indicates 95% confidence interval (1.96×standard deviation) for movement directions observed on non-jump trials. Right panels: trajectories of selected movements that were initiated in a direction intermediate between the original and post-jump target location following 45° (B), 90° (D) and 135° (F) jumps. Line colors indicate data point in corresponding plots to the left. Black circles indicate the position 100ms after movement onset at which point trajectory direction was calculated based on tangential velocity (adjoining black line). The original (pre-jump) target is located at the 12 o’clock position. Gray trajectories illustrate a sample of trajectories from non-jump trials.

Fig 3. Group results for Experiment 1.

Estimated sigmoid parameters across all subjects for each target jump amplitude. A) Total time over which reach direction varied (t ₉₅–t ₀₅; proportional to slope parameter, τ). B) Center of sigmoid, t ₅₀. C) Time required to fully compensate for the target jump, t ₉₅. Error bars indicate s.e.m. D) Average sigmoidal fits to behavior across all subjects obtained by averaging parameters τ and t ₅₀.

Fig 4. Experiment 2 results.

A) Only two target locations were possible within each block, either separated by 45°, or 135°. The target was jumped on 30% of trials. Solid arrow/bold target indicates movement required before target jump. Dashed arrows indicate potential movements required after a target jump. B) Behavior in jump trials and sigmoidal fits trials for a representative subject (green = 45° jump; blue = 135° jump). C)—E) Estimated sigmoid parameters across subjects (as Fig. 3A-C). F) Average sigmoid fits to behavior across all subjects.

Fig 5. Experiment 3 results.

A) The experimental setup was as experiment 1 (Fig. 1A), except that in one condition a series of virtual barriers was put in place to penalize subjects for making intermediate movements. In this experiment, the target only jumped by ±45°, and did so on 30% of trials. Solid arrow/bold target indicates movement required before target jump. Dashed arrows indicate potential movements required after a target jump. B) Behavior on jump trials for a representative subject. Blue points indicate individual trials from the session in which barriers were present. Green points indicate individual trials in which the barriers were absent. Solid lines indicate sigmoidal fit. Shaded region indicates 95% confidence interval for movement direction based on trials from the no-barriers session in which the target did not jump. C)—E) Estimated sigmoid parameters across subjects (as Fig. 3A-C). F) Average sigmoid fit to behavior across all subjects following a target jump.

Fig 6. Computational model.

A) Subjects are uncertain as to the true goal location among two possibilities and expect their beliefs to vary over time. In this case, the subject marginally favors the leftward target at movement onset (p ₀ > ½). During movement, this belief may either strengthen (solid line) or reverse (dashed line). B) When targets are nearby, the optimal course of action is to bias movement only slightly towards the more likely target, allowing greater flexibility later in the movement. C) When targets are widely separated, an intermediate movement is less advantageous. Instead, the optimal course of action is to commit to the more likely target from the outset. D) Predicted initial reach direction (normalized so that 0 corresponds to initial target, and 1 corresponds to the post-jump target) is plotted for a variety of target separations as a function of the initial belief state r ₀. E) As D), but for a model that uses an asymmetric cost function (see Methods).