Modulation of orthogonal body waves enables high maneuverability in sidewinding locomotion

Abstract

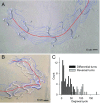
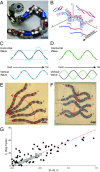
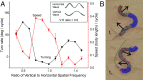
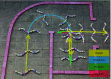
Many organisms move using traveling waves of body undulation, and most work has focused on single-plane undulations in fluids. Less attention has been paid to multiplane undulations, which are particularly important in terrestrial environments where vertical undulations can regulate substrate contact. A seemingly complex mode of snake locomotion, sidewinding, can be described by the superposition of two waves: horizontal and vertical body waves with a phase difference of ± 90°. We demonstrate that the high maneuverability displayed by sidewinder rattlesnakes (Crotalus cerastes) emerges from the animal's ability to independently modulate these waves. Sidewinder rattlesnakes used two distinct turning methods, which we term differential turning (26° change in orientation per wave cycle) and reversal turning (89°). Observations of the snakes suggested that during differential turning the animals imposed an amplitude modulation in the horizontal wave whereas in reversal turning they shifted the phase of the vertical wave by 180°. We tested these mechanisms using a multimodule snake robot as a physical model, successfully generating differential and reversal turning with performance comparable to that of the organisms. Further manipulations of the two-wave system revealed a third turning mode, frequency turning, not observed in biological snakes, which produced large (127°) in-place turns. The two-wave system thus functions as a template (a targeted motor pattern) that enables complex behaviors in a high-degree-of-freedom system to emerge from relatively simple modulations to a basic pattern. Our study reveals the utility of templates in understanding the control of biological movement as well as in developing control schemes for limbless robots.

Keywords: biomechanics; control; robotics; sidewinder; template.

Fig. 1.

Sidewinding in C. cerastes. (A) A sidewinder rattlesnake (C. cerastes) performs sidewinding locomotion on sand. (Inset) A 1- × 2-m fluidized bed trackway filled with sand from the capture locality (Yuma, Arizona); gray arrows indicate airflow used to reset the granular surface using a fluidized bed (see Materials and Methods). (B) A diagram of sidewinding in a snake. Gray regions on the snake’s body indicate regions of static contact with the ground, whereas white regions are lifted and moving. Tracks are shown in gray rectangles. Points on the final snake indicate approximate marker locations used in our experiments. The red arrow indicates direction of motion of the estimated center of mass. (C) Horizontal and vertical body waves during straight sidewinding with the head to the right, as seen in A and B, offset by a phase difference (ϕ) of −90°. Gray regions indicate static contact. The arrow depicts the posterior propagation of waves down the body. Although depicted as sinusoidal waves here, the waves may (and often do) have other forms.

Fig. 2.

Turning behaviors of sidewinder rattlesnakes. (A) Differential turning, shown here using composite frames from overhead video. Blue lines indicate the path of points along the body, and the red line is the path of the approximate center of mass. (B) Reversal turning, shown here using composite frames from overhead video and point paths as in A. (C) Histogram of turn magnitude (change in direction per cycle) for differential and reversal turns. Differential turns resulted in lower changes in direction per cycle than reversal turns, although there was some overlap.

Fig. 3.

Kinematics and hypothesized mechanics of turning behaviors. (A) A diagram of straight sidewinding (gray) followed by differential turning (blue), with the snake turning toward the top left of the page at ${\theta }_d$ degrees per cycle (change in orientation of the approximate center of mass velocity vector). The arc-length distance moved per cycle is $d_1$ for the head and $d_2$ for the tail, although these are reversed when the head is on the inside of the turn, and postural width is L. (B) A diagram of straight sidewinding (gray) followed by reversal turning (green), with the snake turning toward the bottom right of the page at ${\theta }_r$ degrees per cycle. When viewed relative to the direction of motion, the head is initially to the right of the snake’s body, but it is on the left after the reversal turn. (C) Rate of differential turning correlates significantly with displacement difference normalized by length $\left|d_1-d_2\right|/\text{L}$ ($r^2$ = 0.53, $P<0.0001$), with a slope statistically indistinguishable from the theoretical prediction (red line). (D) Difference in horizontal wave phase of the static regions of the snake before and after the turn. The phase changes by almost exactly 180° in reversal turns but does not change in either differential turns or straight locomotion.

Fig. 4.

Robot motions produced by hypothesized turning mechanisms. (A) A 16-joint snake robot capable of sidewinding. (B) Two sequential renderings of the robot during sidewinding, in which the robot adopts an elliptical helix posture produced by the sum of horizontal and vertical sine waves with a ±90° phase difference. Both waves propagate posteriorly, resulting in cyclic, posteriorly propagating regions of lifted movement and static ground contact, without rolling, as in biological sidewinding. (C) Horizontal and vertical waves of the robot during normal sidewinding (black) and differential sidewinding (blue). (D) Horizontal and vertical waves of the robot during normal sidewinding (black) and immediately following reversal turning (green). (E) Differential turning in the robot, shown here using composite frames from overhead video over 17 seconds. The red line indicates the approximate path of the center of mass. (F) Reversal turning in the robot, shown here using composite frames from overhead video over 30 seconds and center of mass path as in E. (G) Comparison of snake (black circles) and robot (gray squares) differential turning with theoretical predictions (red line). Limitations of joint angles and resolutions prevent higher $\left|d_1-d_2\right|/\text{L}$ values for the robot.

Fig. 5.

(A) The effect of varying vertical spatial frequency (relative to horizontal frequency) on speed and turning. (Inset) The waveform of the horizontal and vertical waves at a ratio of 0.6. Gray regions indicate static contact. (B) Two sequential stills 2.3 s apart in Movie S5 of a snake robot performing frequency turning at a ratio of 0.6 (0.14 Hz). Purple-shaded areas are instantaneously static. Black arrows show the direction of motion of moving segments.

Fig. 6.

Images from Movie S6 showing the sidewinder robot moving through a trackway using three turn types (labeled) and straight-line sidewinding. The size of the test course is 3 × 3 m² and the robot completed the course in 48 s.