Response of Polygenic Traits Under Stabilizing Selection and Mutation When Loci Have Unequal Effects
- PMID: 25834214
- PMCID: PMC4478537
- DOI: 10.1534/g3.115.017970
Response of Polygenic Traits Under Stabilizing Selection and Mutation When Loci Have Unequal Effects
Abstract
We consider an infinitely large population under stabilizing selection and mutation in which the allelic effects determining a polygenic trait vary between loci. We obtain analytical expressions for the stationary genetic variance as a function of the distribution of effects, mutation rate, and selection coefficient. We also study the dynamics of the allele frequencies, focusing on short-term evolution of the phenotypic mean as it approaches the optimum after an environmental change. We find that when most effects are small, the genetic variance does not change appreciably during adaptation, and the time until the phenotypic mean reaches the optimum is short if the number of loci is large. However, when most effects are large, the change of the variance during the adaptive process cannot be neglected. In this case, the short-term dynamics may be described by those of a few loci of large effect. Our results may be used to understand polygenic selection driving rapid adaptation.
Keywords: dynamics; genetic variance; mutation; polygenic selection; rapid adaptation; unequal effects.
Copyright © 2015 Jain and Stephan.
Figures

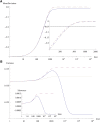
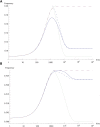


References
-
- Barton N., 1986. The maintenance of polygenic variation through a balance between mutation and stabilizing selection. Genet. Res. 47: 209–216. - PubMed
-
- Barton N., Turelli M., 1987. Adaptive landscapes, genetic distance, and the evolution of quantitative characters. Genet. Res. 49: 157–174. - PubMed
-
- Barton N. H., Keightley P. D., 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3: 11–21. - PubMed
-
- Bürger R., 1991. Moments, cumulants, and polygenic dynamics. J. Math. Biol. 30: 199–213. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
