Optimal ligand descriptor for pocket recognition based on the Beta-shape
- PMID: 25835497
- PMCID: PMC4383629
- DOI: 10.1371/journal.pone.0122787
Optimal ligand descriptor for pocket recognition based on the Beta-shape
Abstract
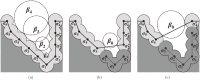
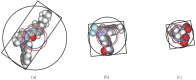
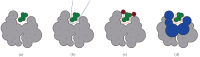
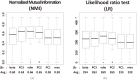
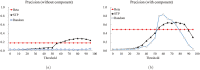
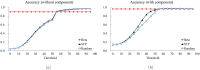
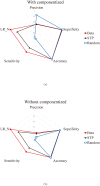
Structure-based virtual screening is one of the most important and common computational methods for the identification of predicted hit at the beginning of drug discovery. Pocket recognition and definition is frequently a prerequisite of structure-based virtual screening, reducing the search space of the predicted protein-ligand complex. In this paper, we present an optimal ligand shape descriptor for a pocket recognition algorithm based on the beta-shape, which is a derivative structure of the Voronoi diagram of atoms. We investigate six candidates for a shape descriptor for a ligand using statistical analysis: the minimum enclosing sphere, three measures from the principal component analysis of atoms, the van der Waals volume, and the beta-shape volume. Among them, the van der Waals volume of a ligand is the optimal shape descriptor for pocket recognition and best tunes the pocket recognition algorithm based on the beta-shape for efficient virtual screening. The performance of the proposed algorithm is verified by a benchmark test.
Conflict of interest statement
Figures

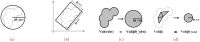


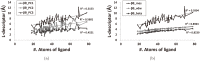

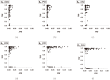







Similar articles
-
SABRE: ligand/structure-based virtual screening approach using consensus molecular-shape pattern recognition.J Chem Inf Model. 2014 Jan 27;54(1):338-46. doi: 10.1021/ci4005496. Epub 2013 Dec 23. J Chem Inf Model. 2014. PMID: 24328054
-
Crystal structure of the vitamin D nuclear receptor ligand binding domain in complex with a locked side chain analog of calcitriol.Arch Biochem Biophys. 2007 Apr 15;460(2):172-6. doi: 10.1016/j.abb.2007.01.031. Epub 2007 Feb 20. Arch Biochem Biophys. 2007. PMID: 17346665
-
BetaDock: shape-priority docking method based on beta-complex.J Biomol Struct Dyn. 2011 Aug;29(1):219-42. doi: 10.1080/07391102.2011.10507384. J Biomol Struct Dyn. 2011. PMID: 21696235
-
Interactions between 1alpha,25(OH)2D3 and residues in the ligand-binding pocket of the vitamin D receptor: a correlated fragment molecular orbital study.J Steroid Biochem Mol Biol. 2010 Jul;121(1-2):63-7. doi: 10.1016/j.jsbmb.2010.03.028. Epub 2010 Mar 15. J Steroid Biochem Mol Biol. 2010. PMID: 20236613
-
Differing shapes of 1 alpha,25-dihydroxyvitamin D3 function as ligands for the D-binding protein, nuclear receptor and membrane receptor: a status report.J Steroid Biochem Mol Biol. 1996 Jan;56(1-6 Spec No):13-22. doi: 10.1016/0960-0760(95)00219-7. J Steroid Biochem Mol Biol. 1996. PMID: 8603033 Review.
Cited by
-
Bioprinting of Vascularized Tissue Scaffolds: Influence of Biopolymer, Cells, Growth Factors, and Gene Delivery.J Healthc Eng. 2019 Apr 2;2019:9156921. doi: 10.1155/2019/9156921. eCollection 2019. J Healthc Eng. 2019. PMID: 31065331 Free PMC article. Review.
References
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

