Survival kinetics of starving bacteria is biphasic and density-dependent

Abstract

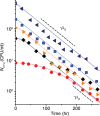
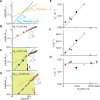
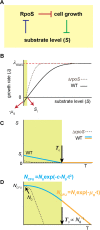
In the lifecycle of microorganisms, prolonged starvation is prevalent and sustaining life during starvation periods is a vital task. In the literature, it is commonly assumed that survival kinetics of starving microbes follows exponential decay. This assumption, however, has not been rigorously tested. Currently, it is not clear under what circumstances this assumption is true. Also, it is not known when such survival kinetics deviates from exponential decay and if it deviates, what underlying mechanisms for the deviation are. Here, to address these issues, we quantitatively characterized dynamics of survival and death of starving E. coli cells. The results show that the assumption--starving cells die exponentially--is true only at high cell density. At low density, starving cells persevere for extended periods of time, before dying rapidly exponentially. Detailed analyses show intriguing quantitative characteristics of the density-dependent and biphasic survival kinetics, including that the period of the perseverance is inversely proportional to cell density. These characteristics further lead us to identification of key underlying processes relevant for the perseverance of starving cells. Then, using mathematical modeling, we show how these processes contribute to the density-dependent and biphasic survival kinetics observed. Importantly, our model reveals a thrifty strategy employed by bacteria, by which upon sensing impending depletion of a substrate, the limiting substrate is conserved and utilized later during starvation to delay cell death. These findings advance quantitative understanding of survival of microbes in oligotrophic environments and facilitate quantitative analysis and prediction of microbial dynamics in nature. Furthermore, they prompt revision of previous models used to analyze and predict population dynamics of microbes.

Fig 1. Temporal survival kinetics of starving E. coli cells.

The number of colony-forming-unit (N _CFU) of glycerol-depleted cultures is plotted over time in a semi-log graph. Different symbols indicate different cell densities at the onset of growth arrest. For clarity, N _CFU of five cultures (with different cell densities) is plotted. See S2 Fig for the complete set of data (also see S8 Fig for the reproducibility of the data). The dashed lines are plotted for a visual guide. The lines have the slope of −μ ₀ (= −0.018 hr ^-1). For the cultures whose densities are higher than ∼10⁸ cells/ml (navy left triangles and blue squares), N _CFU follows single phase exponential decay with the rate of −μ ₀. In the cultures with lower densities, however, we see biphasic kinetics (black diamonds and red circles). Initially, N _CFU decreases gradually (the first phase), and eventually decreases exponentially at the rate of −μ ₀ (the second phase). The solid lines show the fits of our model (discussed further below in the text).

Fig 2. A role of extracellular signaling and rpoS in the density-dependent survival kinetics.

(A) A role of extracellular signaling: a high density of exponentially-growing cells (N _CFU ≈ 7·10⁸/ml) was transferred to a fresh medium without glycerol. N _CFU of cells in the fresh medium (green triangles) decreases similarly to that from the previous experiment (solid blue squares, re-plotted from Fig. 1). Next, a spent medium was prepared from a culture of a high density of cells. N _CFU of cells at low density in the spent medium (green inverse triangles) decreases similarly to that from the previous experiments (solid red circles, re-plotted from Fig. 1). The results indicate that extracellular signaling does not play a role for the density-dependent kinetics. See the text for details. (B) A role of rpoS: Under starvation, N _CFU of the ΔrpoS strain (open symbols) decreases faster than that of the wild type strain (solid symbols, re-plotted from Fig. 1); compare the slope of the dotted line −μ₀ ^ΔrpoS (= −0.035 hr ^-1) and the slope of the dashed line −μ ₀ (= −0.018 hr ^-1). See also S6 Fig for N _CFU of other densities of the ΔrpoS strain. Importantly, in the low cell-density cultures (e.g., open red circles), the periods during which N _CFU is maintained are much shorter for the ΔrpoS strain (brown region) than for the wild type strain (green region); note that here the brown and green regions are approximately determined as regions where the survival kinetics does not follow exponentially decay. This indicates that rpoS plays an important role for the wild type strain to maintain N _CFU for extended periods of time in low density under starvation.

Fig 3. Quantitative analyses of the survival kinetics of wild type cells.

(A) The log-log plot of log (N ₀ /N _CFU), where N ₀ is the number of CFU at the time zero, reveals the power law exponent of exponential functions; see the text, and Eqs (1) and (2). (B) At high cell density, N _CFU of the wild type cells plotted as described above follows a straight line with a slope of 1, indicating that the survival kinetics can be described by Eq. (1); see also S7A Fig for another high cell density. (C-D) At lower cell density (see also S7C Fig—S7E Fig for other low cell densities), the slope is initially 2 (green region), but becomes 1 later, revealing the biphasic decay seen in Fig. 1. The time at which the transition occurs is marked as T ₀ (arrows). Numerically, T ₀ is obtained from the time point at which the orange line and the cyan dashed line intersect. Note that T ₀ is greater for lower density. (E) T₀ ⁻¹ is linearly proportional to N ₀. (F, G) We obtained the coefficients c ₁ and c ₂ in Eqs (1) and (2) by fitting the second phase and the first phase of the biphasic decay respectively. Note that for high cell densities which show a single-phase decay, we used Eq. (1) to fit the entire range, and c ₂ is not available. We see that c ₂ increases linearly to N ₀ (c ₂ ∝ N ₀) in Fig. 3F. In Fig. 3G, we see c ₁ remains constant for different N ₀. The dashed lines are plotted for a visual guide.

Fig 4. A mechanistic account of the density-dependent, biphasic survival kinetics.

(A) Cells consume substrates for cell growth and the substrate concentration decreases in the medium (green line). When the concentration decreases to the levels affecting the rate of cell growth, RpoS accumulates (blue line) [26,27]. RpoS represses cell growth (red line) [–32], forming negative feedback. In the feedback scheme, at low substrate levels, RpoS strongly represses cell growth and hence, substrate consumption, allowing cells to conserve a small amount of the substrate before it is completely depleted by cell growth. See the text for details. (B) This feedback predicts that as the substrate concentration is reduced, the growth arrest occurs at a non-zero substrate concentration S ₁, i.e., λ = 0 at S = S ₁ > 0. This prediction agrees with previous studies [–35]. Importantly, further studies show that although the growth rate of the population is zero at S = S ₁, the substrate consumption rate is not zero; see [36] for review. This is commonly known as maintenance requirement; it requires continuous influx of the substrate to maintain a constant population size (λ = 0). If the influx of the substrate is less than the level needed for the maintenance, λ < 0 (green region) [37,38]. Our model indicates that λ(0) = − μ ₀; see the text for details. As a comparison, the relation of λ and S in the ΔrpoS strain is shown as a dashed line. Note that at intermediate substrate concentrations, λ of ΔrpoS strain is higher than that of the wild type strain [–32]. Also, note that when the substrate is completely exhausted, the culture of the ΔrpoS strain loses viability more rapidly than the wild type strain (see [18,25] and Fig. 2B); thus, the value of λ(0) of ΔrpoS strain should be less than that of the wild type strain. (C, D) At the onset of growth arrest (time zero in S1B Fig), S = S ₁; see Fig. 4B. Without additional influx of the substrate, S will continue to decrease over time due to the consumption for the maintenance (cyan line in green region in Fig. 4C). Following the relation between λ and S depicted in Fig. 4B, λ will continue to decrease over time too. This will result in gradual decrease of N _CFU (cyan line in green region in Fig. 4D). At some point (T ₀), the substrate gets completely depleted (orange line in Fig. 4C) and N _CFU decreases exponentially at a fixed rate of λ (0) afterwards (orange line in Fig. 4D). For the culture with higher cell-densities, S will decrease faster because the substrate is consumed by more cells, leading to shorter periods of the first phase. Quantitative formulation of these processes straightforwardly leads to a mathematical solution equal to the empirical formulas (Eqs (3) and (4)). The solid lines in Fig. 1 and S2 Fig show the fits of the solution to the data. See the text for details.