Systematic evaluation of an atomic clock at 2 × 10(-18) total uncertainty
- PMID: 25898253
- PMCID: PMC4411304
- DOI: 10.1038/ncomms7896
Systematic evaluation of an atomic clock at 2 × 10(-18) total uncertainty
Abstract
The pursuit of better atomic clocks has advanced many research areas, providing better quantum state control, new insights in quantum science, tighter limits on fundamental constant variation and improved tests of relativity. The record for the best stability and accuracy is currently held by optical lattice clocks. Here we take an important step towards realizing the full potential of a many-particle clock with a state-of-the-art stable laser. Our (87)Sr optical lattice clock now achieves fractional stability of 2.2 × 10(-16) at 1 s. With this improved stability, we perform a new accuracy evaluation of our clock, reducing many systematic uncertainties that limited our previous measurements, such as those in the lattice ac Stark shift, the atoms' thermal environment and the atomic response to room-temperature blackbody radiation. Our combined measurements have reduced the total uncertainty of the JILA Sr clock to 2.1 × 10(-18) in fractional frequency units.
Figures
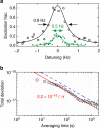
 . The error bars represent the 1σ uncertainty in the total deviation estimator, calculated assuming a white noise process, which is valid after the atomic servo attack time of ≈30 s.
. The error bars represent the 1σ uncertainty in the total deviation estimator, calculated assuming a white noise process, which is valid after the atomic servo attack time of ≈30 s.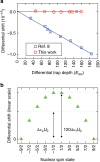


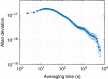
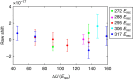
References
-
- Bloom B. J. et al. An optical lattice clock with accuracy and stability at the 10−18 level. Nature 506, 71–75 (2014). - PubMed
-
- Chou C. W., Hume D. B., Koelemeij J. C. J., Wineland D. J. & Rosenband T. Frequency comparison of two high-accuracy Al+ optical clocks. Phys. Rev. Lett. 104, 070802 (2010). - PubMed
-
- Hinkley N. et al. An atomic clock with 10−18 instability. Science 341, 1215–1218 (2013). - PubMed
-
- Madej A. A., Dubé P., Zhou Z., Bernard J. E. & Gertsvolf M. 88Sr+ 445-THz Single-ion reference at the 10−17 level via control and cancellation of systematic uncertainties and its measurement against the SI second. Phys. Rev. Lett. 109, 203002 (2012). - PubMed
-
- Ushijima I., Takamoto M., Das M., Ohkubo T. & Katori H. Cryogenic optical lattice clocks. Nat. Photonics 9, 185–189 (2015).
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
Research Materials

