Comparing denominator degrees of freedom approximations for the generalized linear mixed model in analyzing binary outcome in small sample cluster-randomized trials

Abstract

Background: Small number of clusters and large variation of cluster sizes commonly exist in cluster-randomized trials (CRTs) and are often the critical factors affecting the validity and efficiency of statistical analyses. F tests are commonly used in the generalized linear mixed model (GLMM) to test intervention effects in CRTs. The most challenging issue for the approximate Wald F test is the estimation of the denominator degrees of freedom (DDF). Some DDF approximation methods have been proposed, but their small sample performances in analysing binary outcomes in CRTs with few heterogeneous clusters are not well studied.

Methods: The small sample performances of five DDF approximations for the F test are compared and contrasted under CRT frameworks with simulations. Specifically, we illustrate how the intraclass correlation (ICC), sample size, and the variation of cluster sizes affect the type I error and statistical power when different DDF approximation methods in GLMM are used to test intervention effect in CRTs with binary outcomes. The results are also illustrated using a real CRT dataset.

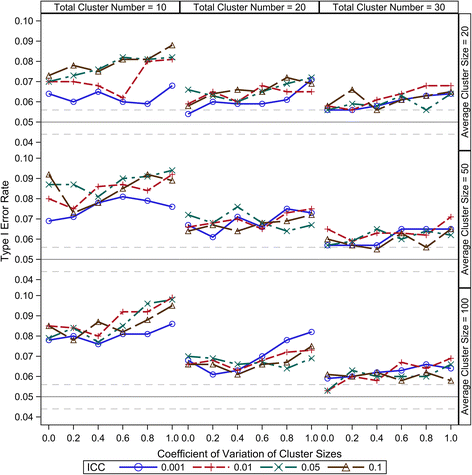
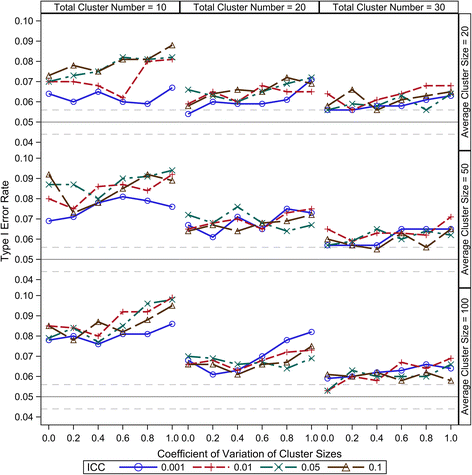
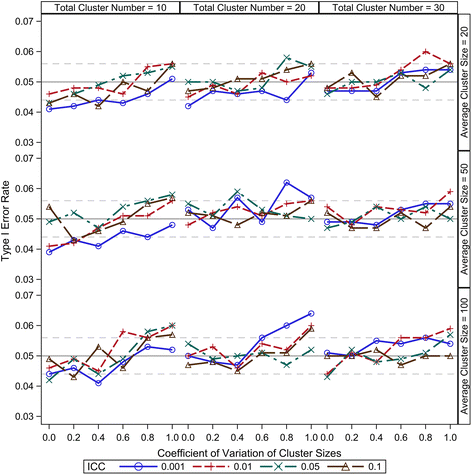
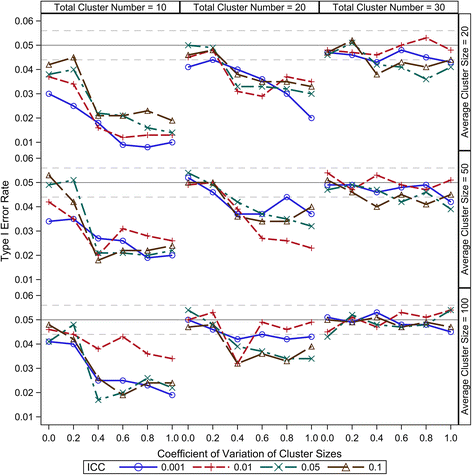
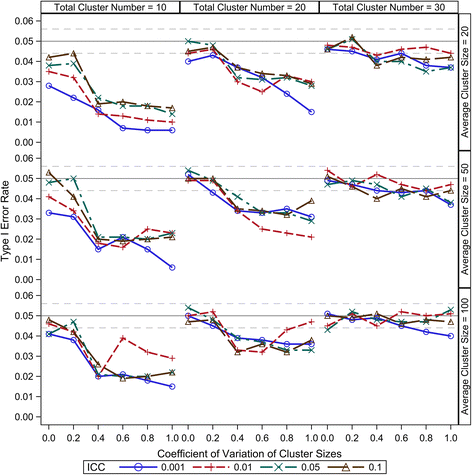
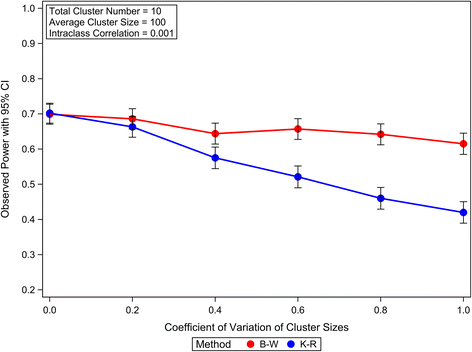
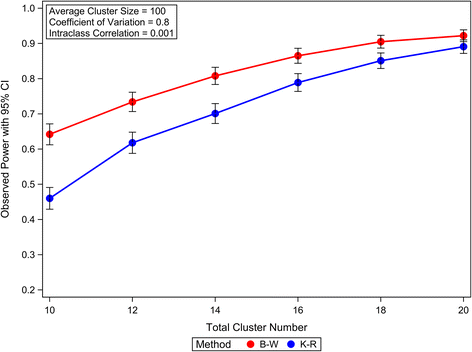
Results: Our simulation results suggest that the Between-Within method maintains the nominal type I error rates even when the total number of clusters is as low as 10 and is robust to the variation of the cluster sizes. The Residual and Containment methods have inflated type I error rates when the cluster number is small (<30) and the inflation becomes more severe with increased variation in cluster sizes. In contrast, the Satterthwaite and Kenward-Roger methods can provide tests with very conservative type I error rates when the total cluster number is small (<30) and the conservativeness becomes more severe as variation in cluster sizes increases. Our simulations also suggest that the Between-Within method is statistically more powerful than the Satterthwaite or Kenward-Roger method in analysing CRTs with heterogeneous cluster sizes, especially when the cluster number is small.

Conclusion: We conclude that the Between-Within denominator degrees of freedom approximation method for F tests should be recommended when the GLMM is used in analysing CRTs with binary outcomes and few heterogeneous clusters, due to its type I error properties and relatively higher power.

Figure 1

Observed type I error rates of GLMM Wald F test with Residual approximation of denominator degrees of freedom. The type I error rates are calculated from 5000 independent simulation replicates. The solid grey lines indicate the nominal level and the dashed grey lines indicate the upper and lower bounds of the 95% confident interval.

Figure 2

Observed type I error rates of GLMM Wald F test with Containment approximation of denominator degrees of freedom. The type I error rates are calculated from 5000 independent simulation replicates. The solid grey lines indicate the nominal level and the dashed grey lines indicate the upper and lower bounds of the 95% confident interval.

Figure 3

Observed type I error rates of GLMM Wald F test with Between-Within approximation of denominator degrees of freedom. The type I error rates are calculated from 5000 independent simulation replicates. The solid grey lines indicate the nominal level and the dashed grey lines indicate the upper and lower bounds of the 95% confident interval.

Figure 4

Observed type I error rates of GLMM Wald F test with Satterthwaite approximation of denominator degrees of freedom. The type I error rates are calculated from 5000 independent simulation replicates. The solid grey lines indicate the nominal level and the dashed grey lines indicate the upper and lower bounds of the 95% confident interval.

Figure 5

Observed type I error rates of GLMM Wald F test with Kenward-Roger approximation of denominator degrees of freedom. The type I error rates are calculated from 5000 independent simulation replicates. The solid grey lines indicate the nominal level and the dashed grey lines indicate the upper and lower bounds of the 95% confident interval.

Figure 6

The effects of variation of cluster sizes on the power of GLMM Wald F tests in analyzing CRTs with few heterogeneous clusters. The observed powers and the 95% confidence intervals are calculated from 1000 independent simulation replicates.

Figure 7

The diminished power loss of GLMM Wald F test with Kenward-Roger approximation of denominator degrees of freedom with the increase of cluster number in analyzing CRTs with few heterogeneous clusters. The observed powers and the 95% confidence intervals are calculated from 1000 independent simulation replicates.