Approximate joint diagonalization and geometric mean of symmetric positive definite matrices

Abstract

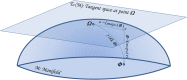
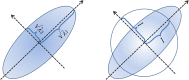
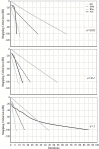
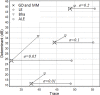
We explore the connection between two problems that have arisen independently in the signal processing and related fields: the estimation of the geometric mean of a set of symmetric positive definite (SPD) matrices and their approximate joint diagonalization (AJD). Today there is a considerable interest in estimating the geometric mean of a SPD matrix set in the manifold of SPD matrices endowed with the Fisher information metric. The resulting mean has several important invariance properties and has proven very useful in diverse engineering applications such as biomedical and image data processing. While for two SPD matrices the mean has an algebraic closed form solution, for a set of more than two SPD matrices it can only be estimated by iterative algorithms. However, none of the existing iterative algorithms feature at the same time fast convergence, low computational complexity per iteration and guarantee of convergence. For this reason, recently other definitions of geometric mean based on symmetric divergence measures, such as the Bhattacharyya divergence, have been considered. The resulting means, although possibly useful in practice, do not satisfy all desirable invariance properties. In this paper we consider geometric means of covariance matrices estimated on high-dimensional time-series, assuming that the data is generated according to an instantaneous mixing model, which is very common in signal processing. We show that in these circumstances we can approximate the Fisher information geometric mean by employing an efficient AJD algorithm. Our approximation is in general much closer to the Fisher information geometric mean as compared to its competitors and verifies many invariance properties. Furthermore, convergence is guaranteed, the computational complexity is low and the convergence rate is quadratic. The accuracy of this new geometric mean approximation is demonstrated by means of simulations.

Fig 1. Symmetric positive definite matrices, e.g. covariance matrices, are constrained by their symmetry, the strict positivity of the diagonal elements (variance) and the Cauchy-Schwarz inequalities bounding the absolute value of the off-diagonal elements: |Cov(x_ix_j)|≤[Var(x_j)Var(x_j)]^1/2, for all i,j∈{1,…,N}.

This topology is easily visualized in case of 2x2 matrices; any 2x2 covariance matrix can be seen as a point in 3D Euclidean space, with two coordinates given by the two variances (diagonal elements) and the third coordinate given by the covariance (either one of the off-diagonal element). By construction a covariance matrix must stay within the cone boundaries. As soon as the point touches the boundary of the cone, the matrix is no more positive definite.

Fig 2. The Manifold and the tangent space at a point.

Consider a point Ω on M and construct the tangent space T_ΩM on it. Now take a tangent vector V departing from Ω, which is our reference point. There exists one and only one geodesic on the manifold starting at Ω that corresponds to V; think at rolling the plane (tangent space) on the surface (manifold) in such a way that the vector always touches the surface. The end point on M is Φ. We see that the geodesics on M through Ω are transformed into straight lines and the distances along all geodesics are preserved (this is true in the neighborhood of Ω). (Rearranged from [17]).

Fig 3. The ellipsoids in the figure are isolines of constant density of bivariate Gaussian distributions.

The semiaxes are proportional to the square root of the eigenvalues of the covariance matrix. If we ask how far the ellipsoid is from the circle, which is the definition of the norm (12), we see that an eigenvalue = 2 contribute to the distance from the identity as much as an eigenvalue = 1/2 does, as one would expect, since the eigenvalues are squared quantities. Neither the sum nor the sum of the logarithm of the eigenvalue verify this property.

Fig 4. Zoom on the manifold as it is represented in Fig 2.

Consider two points Ω ₁ and Ω ₂ on M and construct the tangent space T_ΩM through the current estimation of their mean M, initialized as the arithmetic mean. At each iteration, the algorithm maps the points on the tangent space, computes the mean vector and maps back the point on the manifold. At each iteration the estimation of the mean is updated, thus the point of transition into the tangent space changes, until convergence, that is, until this transition point will not change anymore, coinciding with the geometric mean, that is, satisfying (23).

Fig 5. Typical convergence behavior of algorithms GM, MM, Bha and ALE (first part of ALE algorithm, corresponding to AJD estimation by Pham’s algorithm).

The simulations are done generating data according to (40) for three noise levels (σ = 0.01, 0.1, 1). Each algorithm was stopped when its own stopping criterion became smaller than -100dB.

Fig 6. Typical relation between the trace (x-axis) and the determinant (y-axis, in dB) of the FI geometric mean as estimated with algorithm GD and MM (cross), and the means estimated by LE (diamond), Bha (triangle) and ALE (disk) for four noise levels (σ = 0.01, 0.05, 0.1 0.2), N = 10 and K = 100.

The arrows link the FI estimation with the corresponding LE and Bha estimations.

Fig 7. Distance of the LE (diamonds), Bha (triangles) and ALE (disks) geometric mean to the FI geometric mean estimated by the GD and MM algorithm (they converge to the same point), for three noise levels (σ = 0.01, 0.1, 1) and variable condition numbers of the true mixing matrix in (40).

The simulations were repeated 100 times, with N = 10 and K = 100. Notice the different scales on the y-axes.