Non-convexly constrained image reconstruction from nonlinear tomographic X-ray measurements

Abstract

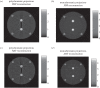
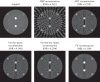
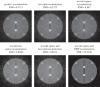
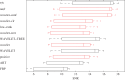
The use of polychromatic X-ray sources in tomographic X-ray measurements leads to nonlinear X-ray transmission effects. As these nonlinearities are not normally taken into account in tomographic reconstruction, artefacts occur, which can be particularly severe when imaging objects with multiple materials of widely varying X-ray attenuation properties. In these settings, reconstruction algorithms based on a nonlinear X-ray transmission model become valuable. We here study the use of one such model and develop algorithms that impose additional non-convex constraints on the reconstruction. This allows us to reconstruct volumetric data even when limited measurements are available. We propose a nonlinear conjugate gradient iterative hard thresholding algorithm and show how many prior modelling assumptions can be imposed using a range of non-convex constraints.

Keywords: compressed sensing; inverse problems; nonlinear constrained optimization; tomography.

Figure 1.

A simulated phantom made up of four materials which at 80 keV have mass attenuation coefficients of 0.2, 0.23, 2.77 and 4.46 cm² g⁻¹, respectively. To show the difference between the two low-attenuating materials, the grey scale has been compressed (see colourbar).

Figure 2.

Reconstruction of the simulated phantom using two algorithms (the FBP algorithm and the ART). The reconstructions in (a,c) use simulations of a polychromatic X-ray source, whereas the reconstructions in (b,d) use a monochromatic source. To show the difference between the two low-attenuating materials, the grey scale has been compressed (see colourbar).

Figure 3.

Reconstruction of the simulated phantom from polychromatic X-ray measurements by optimizing equation (2.8).

Figure 4.

Comparison of linear reconstruction methods on a challenging phantom from 40 projections. The original is an object of aluminium, silicon, gold and silver. FBP gives a reconstruction with severe artefacts and of the iterative solvers, the TV regularized method performs best.

Figure 5.

Comparison of nonlinear reconstruction methods on a challenging phantom from 40 projections. The original is an object of aluminium, silicon, gold and silver. The nonlinear reconstruction performs better under certain constraints than the linear methods. The best-performing non-convex constraint is the combination of wavelet sparsity with a non-negative matrix factorization. When using wavelet-sparsity here, we use a row sparse matrix model as described in §3b(ii).

Figure 6.

Distribution of results for different methods and for 10 different material assignments, where each area in the phantom is assigned a single material. The seven methods shown in red (light grey in print version) (lower case labels) use the nonlinear model in the reconstruction, while the other five methods (upper case labels) use the linear model. From top to bottom, the methods are constraint using (1) non-negative matrix factorization projections, (2) mixed wavelet sparsity and non-negative matrix factorization projections, (3) mixed wavelet sparsity and low-rank matrix factorization projections, (4) wavelet tree sparsity, (5) wavelet sparsity, (6) low-rank matrix projections, (7) positivity, (8) total variation regularization, (9) wavelet tree sparsity and (10) wavelet sparsity. The second to last results are those achieved with ART [1] and the last results are those for FBP. (Online version in colour.)

Figure 7.

Distribution of results for different methods and for 10 different material assignments, where each area in the phantom is assigned a random mixture of all three materials. The seven methods shown in red (light grey in print version) (lower case labels) use the nonlinear model in the reconstruction, while the other five methods (upper case labels) use the linear model. From top to bottom, the methods are constraint using (1) non-negative matrix factorization projections, (2) mixed wavelet sparsity and non-negative matrix factorization projections, (3) mixed wavelet sparsity and low-rank matrix factorization projections, (4) wavelet tree sparsity, (5) wavelet sparsity, (6) low-rank matrix projections, (7) positivity, (8) total variation regularization, (9) wavelet tree sparsity and (10) wavelet sparsity. The second to last results are those achieved with ART [1] and the last results are those for FBP. (Online version in colour.)

Figure 8.

FBP reconstruction from 32 projections of a slice through a model engine block made of aluminium.

Figure 9.

Reconstruction with the nonlinear model and a sparsity and non-negative matrix factorization constraint. Reconstruction from 32 projections of a slice through a model engine block made of aluminium.

Figure 10.

Detail of two reconstructions from 200 projections. (a) FBP and (b) nonlinear conjugate gradient reconstructions of a slice through a high-density workpiece with internal structures. Beam-hardening artefacts are visible in the FBP reconstruction which are not visible in the reconstruction achieved with our approach. (Online version in colour.)