Neuronal morphology generates high-frequency firing resonance

Abstract

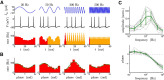
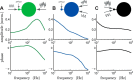
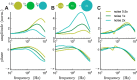
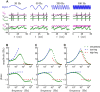
The attenuation of neuronal voltage responses to high-frequency current inputs by the membrane capacitance is believed to limit single-cell bandwidth. However, neuronal populations subject to stochastic fluctuations can follow inputs beyond this limit. We investigated this apparent paradox theoretically and experimentally using Purkinje cells in the cerebellum, a motor structure that benefits from rapid information transfer. We analyzed the modulation of firing in response to the somatic injection of sinusoidal currents. Computational modeling suggested that, instead of decreasing with frequency, modulation amplitude can increase up to high frequencies because of cellular morphology. Electrophysiological measurements in adult rat slices confirmed this prediction and displayed a marked resonance at 200 Hz. We elucidated the underlying mechanism, showing that the two-compartment morphology of the Purkinje cell, interacting with a simple spiking mechanism and dendritic fluctuations, is sufficient to create high-frequency signal amplification. This mechanism, which we term morphology-induced resonance, is selective for somatic inputs, which in the Purkinje cell are exclusively inhibitory. The resonance sensitizes Purkinje cells in the frequency range of population oscillations observed in vivo.

Keywords: Purkinje cell; computational modelling; information bandwidth; neural dynamics.

Figure 1.

Electrical circuit equivalent to the two-compartment model: g_e is the conductance of the electrode, g_s and C_s are the conductance and capacitance of the somatic compartment, g_d and C_d are the conductance and capacitance of the dendritic compartment, and g_j is the junctional conductance between the two compartments.

Figure 2.

Firing modulation elicited by sinusoidal input currents in Purkinje cell models of different complexities. A, Illustration of the protocol for the measurement of the firing-rate modulation at a given frequency: a sinusoidal current of frequency f (top row) is injected into a single-compartment model cell on top of a noisy background (data not shown); spike times are recorded over many repetitions of the input (middle row) and used to estimate the instantaneous firing rate (bottom row). B, The modulation of the firing rate over one period of the input is well described by a sinusoidal variation around the mean firing rate at the frequency f of the input; the amplitude and phase of the corresponding sinusoidal fit are used to quantify the modulation. The data shown in A and B was obtained from a single-compartment EIF model with a noisy background input leading to a mean firing rate of 30 Hz with a CV of 0.8 (membrane potential SD of 6 mV). C, Amplitude (normalized by the mean firing rate) and phase of the firing modulation as function of the input frequency, for three different models of the Purkinje cell: (1) a multicompartment conductance-based model (left); (2) a single-compartment conductance-based model (middle); and (3) a single-compartment EIF model (right). The mean firing rate was set to 30 Hz in the three models. Note that, here and in the following figures, we do not consider firing-rate modulations <10 Hz. This low-frequency range is known to be shaped by the specific conductances of the cell and is not the focus of the present work.

Figure 3.

Boosting of high-frequency firing modulation in Purkinje cells in vitro. A, Example of recorded responses in a typical cell. Top, Injected current waveforms; middle, modulation of the membrane potential in a single trial; bottom, instantaneous firing rate estimated by averaging over trials. B, Sinusoidal fits to the single period average of the firing-rate modulation shown in A. C, Amplitude (normalized by the mean firing rate) and phase of the firing modulation as a function of the input frequency; mean ± SD. Dashed lines, Individual cells (n = 10 cells from 4 animals); green lines, averages. The mean firing rate was 46 ± 22 Hz.

Figure 4.

Subthreshold dynamics of the Purkinje cell. A, Membrane potential dynamics (bottom) elicited by a current chirp (top). B, Amplitude (top) and phase (bottom) of the complex impedance Z of the cell determined from A as a function of input frequency compared with the impedances of single- and two-compartment models. C, Current response (top) to a step of holding potential (bottom) in voltage clamp. Inset, Zoom on the first 5 ms. The green trace is a fit by a two-compartment model symbolized here and subsequently by an asymmetric dumbbell (green).

Figure 5.

Firing modulation in the two-compartment EIF model. Amplitude (top) and phase (bottom) of the firing modulation as a function of the frequency of the input, elicited in three different conditions. A, Input injected in the somatic compartment, background noise injected in both compartments. B, Input injected in the dendritic compartment, background noise injected in both compartments. C, Input injected in the somatic compartment, background noise injected in the somatic compartment only. The amplitude of the background noise was adjusted to produce the same interspike interval CV as in A and B. The mean firing rate was 45 Hz in all three cases.

Figure 6.

Morphology shapes the high-frequency resonance. A, Influence of somatic compartment area on the firing modulation. The mean firing rates are 49, 45, and 35 Hz for increasing area. B, Influence of dendritic compartment area on the firing modulation. The mean firing rate was 45 Hz in all three cases. C, Influence of synaptic noise in the dendritic compartment area on the firing modulation. The mean firing rates are 55, 45, and 30 Hz for increasing noise. At low noise, resonances at multiples of the firing rate become visible. The location of these additional resonances is independent of the location of the main, high-frequency resonance. In each panel, a single parameter was increased/decreased by a factor of 2, with all other parameter values kept as in Figure 5A (1× condition). For comparison, the firing modulation amplitude was normalized to the values at 1 Hz. In B, the mean and variance of the input were adjusted to keep the firing rate at 45 Hz and CV at 0.7.

Figure 7.

A, Illustration of the mapping from a two-compartment model to an effective single-compartment model. Top, Injected current; middle, membrane potential dynamics in the somatic and dendritic compartments (note the similarity in the fluctuations); bottom, membrane potential in the dendritic compartment compared with the effective, oscillating threshold. B–D, Comparison between analytical results and simulations for three different values of the dendritic reset β. B, β = 0.5 mV as in Figure 5. C, β = 3 mV. D, β = 10 mV. All other parameters as in Figure 5. In B, the analytical curves were obtained by setting the mean input so as to reproduce the target firing rate of 45 Hz (the equivalent single-compartment model does not produce the correct current to rate relationship because β is close to the AP onset range Δ_T). In C and D, there are no free parameters in the analytical results.

Figure 8.

High-frequency resonance in a Purkinje cell with an artificial threshold. A, Diagram illustrating the artificial firing mechanism used to evaluate Purkinje cell firing in the absence of native voltage-dependent conductances. They were blocked, and an electronic threshold was imposed on the recorded membrane potential. Whenever the threshold was crossed, the membrane potential was reset by a hyperpolarizing current pulse summed with the ongoing sine wave and noise stimuli. B, Example of injected current (top) and the resulting membrane potential dynamics (bottom). APs (in red) occur at times when the membrane potential crosses the threshold value (dashed line). C, Amplitude (normalized by the mean firing rate) and phase of the firing modulation as a function of the input frequency; mean ± SD. Dashed lines, Individual cells (n = 6 cells); green lines, averages. The mean firing rate was 12 ± 2 Hz.