Genetic Variability Under the Seedbank Coalescent

Abstract

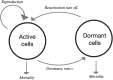
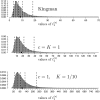
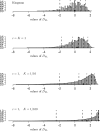
We analyze patterns of genetic variability of populations in the presence of a large seedbank with the help of a new coalescent structure called the seedbank coalescent. This ancestral process appears naturally as a scaling limit of the genealogy of large populations that sustain seedbanks, if the seedbank size and individual dormancy times are of the same order as those of the active population. Mutations appear as Poisson processes on the active lineages and potentially at reduced rate also on the dormant lineages. The presence of "dormant" lineages leads to qualitatively altered times to the most recent common ancestor and nonclassical patterns of genetic diversity. To illustrate this we provide a Wright-Fisher model with a seedbank component and mutation, motivated from recent models of microbial dormancy, whose genealogy can be described by the seedbank coalescent. Based on our coalescent model, we derive recursions for the expectation and variance of the time to most recent common ancestor, number of segregating sites, pairwise differences, and singletons. Estimates (obtained by simulations) of the distributions of commonly employed distance statistics, in the presence and absence of a seedbank, are compared. The effect of a seedbank on the expected site-frequency spectrum is also investigated using simulations. Our results indicate that the presence of a large seedbank considerably alters the distribution of some distance statistics, as well as the site-frequency spectrum. Thus, one should be able to detect from genetic data the presence of a large seedbank in natural populations.

Keywords: Wright–Fisher model; distance statistics; dormancy; seedbank coalescent; site-frequency spectrum.

Figure 1

Realization of a seedbank coalescent with all $n=8$ sampled lineages assumed active. Mutations are, in this example, allowed to occur only on active ancestral lineages represented by solid lines; ancestral lineages residing in the seedbank are represented by dotted lines. Coalescences are allowed only among active lineages.

Figure 2

Dynamics of reversible microbial dormancy, according to Jones and Lennon (2010).

Figure 3

Estimates of the normalized site-frequency spectrum ${\varphi }_i^{\left(n\right)}=\mathbb{E}\left[{\xi }_i^{\left(n\right)}\right]/\mathbb{E}\left[\left|{\xi }^{\left(n\right)}\right|\right]$ with all $n=100$ sampled lines assumed active and values of c and K as shown $\left(d=0\right)$. The mutation rate in the active population is fixed, ${\theta }_1=2$, and there is no mutation in the dormant states $\left({\theta }_2=0\right)$. All estimates based on ${10}^5$ replicates.

Figure 4

Estimates of the distribution of the ${\ell }_2^{\left(n\right)}$ statistic (Equation 23), with all $n=100$ sampled lines assumed active, c and K as shown, ${\theta }_1=2$, and ${\theta }_2=0.$ The vertical dashed lines are the $5\text{\%,}$ $25\text{\%,}$ $50\text{\%,}$ $75\text{\%,}$ and $95\text{\%}$ quantiles and the solid square (■) denotes the mean. The entries are normalized to have unit mass 1. All estimates are based on ${10}^5$ replicates.

Figure 5

Estimates of the distribution of Tajima’s $D_{\mathrm{T}}$ (Equation 24) with all $n=100$ sampled lines assumed active, ${\theta }_1=2$, and ${\theta }_2=0.$ The vertical dashed lines are the $5\text{\%,}$ $25\text{\%,}$ $50\text{\%,}$ $75\text{\%,}$ and $95\text{\%}$ quantiles and the solid square (■) denotes the mean. The entries are normalized to have unit mass 1. The histograms are drawn on the same horizontal scale. Estimates are based on ${10}^5$ replicates.

Figure 6

Estimates of the distribution of Fu and Li’s $D_{\mathrm{FL}}$ (Equation 25) with all $n=100$ sampled lines assumed active, ${\theta }_1=2$, and ${\theta }_2=0.$ The vertical dashed lines are the $5\text{\%,}$ $25\text{\%,}$ $50\text{\%,}$ $75\text{\%,}$ and $95\text{\%}$ quantiles and the solid square (■) denotes the mean. The entries are normalized to have unit mass 1. The histograms are drawn on the same horizontal scale. Estimates are based on ${10}^5$ replicates.

Figure 7

Estimates of the distribution of Fay and Wu’s $D_{\mathrm{FW}}$ (Equation 26) with all $n=100$ sampled lines assumed active, ${\theta }_1=2$, and ${\theta }_2=0.$ The vertical dashed lines are the $5\text{\%,}$ $25\text{\%,}$ $50\text{\%,}$ $75\text{\%,}$ and $95\text{\%}$ quantiles and the solid square (■) denotes the mean. The entries are normalized to have unit mass 1. The histograms are drawn on the same horizontal scale. Estimates are based on ${10}^5$ replicates.