Utility of characters evolving at diverse rates of evolution to resolve quartet trees with unequal branch lengths: analytical predictions of long-branch effects

Abstract

Background: The detection and avoidance of "long-branch effects" in phylogenetic inference represents a longstanding challenge for molecular phylogenetic investigations. A consequence of parallelism and convergence, long-branch effects arise in phylogenetic inference when there is unequal molecular divergence among lineages, and they can positively mislead inference based on parsimony especially, but also inference based on maximum likelihood and Bayesian approaches. Long-branch effects have been exhaustively examined by simulation studies that have compared the performance of different inference methods in specific model trees and branch length spaces.

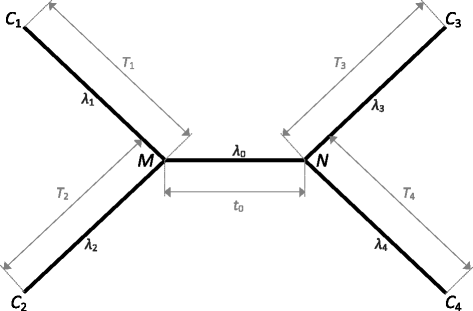
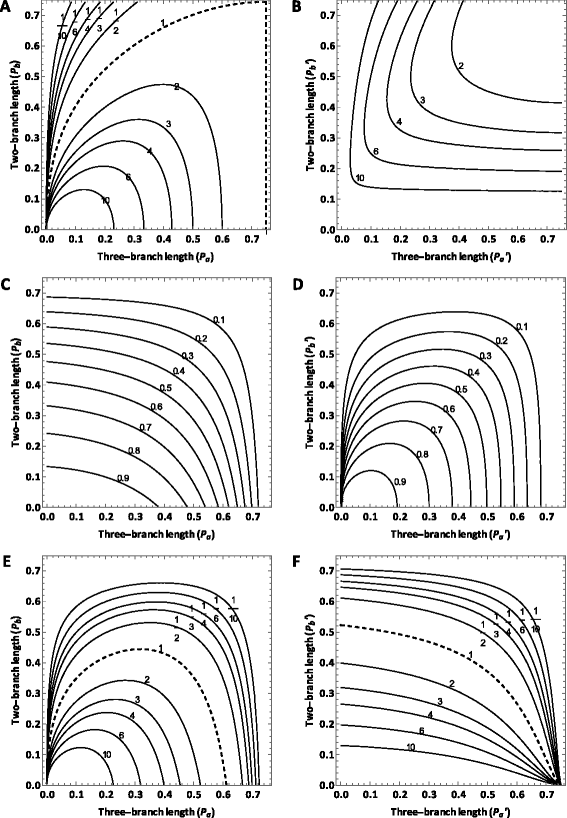
Results: In this paper, by generalizing the phylogenetic signal and noise analysis to quartets with uneven subtending branches, we quantify the utility of molecular characters for resolution of quartet phylogenies via parsimony. Our quantification incorporates contributions toward the correct tree from either signal or homoplasy (i.e. "the right result for either the right reason or the wrong reason"). We also characterize a highly conservative lower bound of utility that incorporates contributions to the correct tree only when they correspond to true, unobscured parsimony-informative sites (i.e. "the right result for the right reason"). We apply the generalized signal and noise analysis to classic quartet phylogenies in which long-branch effects can arise due to unequal rates of evolution or an asymmetrical topology. Application of the analysis leads to identification of branch length conditions in which inference will be inconsistent and reveals insights regarding how to improve sampling of molecular loci and taxa in order to correctly resolve phylogenies in which long-branch effects are hypothesized to exist.

Conclusions: The generalized signal and noise analysis provides analytical prediction of utility of characters evolving at diverse rates of evolution to resolve quartet phylogenies with unequal branch lengths. The analysis can be applied to identifying characters evolving at appropriate rates to resolve phylogenies in which long-branch effects are hypothesized to occur.

Figure 1

An unrooted four-taxon tree in an ultrametric form, with an internode of length (in time) t ₀ and four subtending branches of lengths (in time) T ₁, T ₂, T ₃, and T ₄. The ancestral states of a molecular character at the two ends of the internode are denoted as M and N. The character states at the terminal tips of the four subtending branches are denoted as C ₁, C ₂, C ₃, and C ₄. The average substitution rate of the character over the internode and the four subtending branches is denoted as λ ₀, λ ₁, λ ₂, λ ₃, and λ ₄. The expected number of character state changes in the internode and the four subtending branches are thus given by λ ₀ t ₀, λ ₁ T ₁, λ ₂ T ₂, λ ₃ T ₃, and λ ₄ T ₄, respectively.

Figure 2

Two classic quartet branch length conditions in which long-branch effects can arise. A) Four-taxon tree modeled by Huelsenbeck and Hillis [22]. The internode and two subtending branches labeled a are constrained to have the same length (i.e. “three-branch length”), so are the two subtending branches labeled b (i.e. “two-branch length”); p _a and p _b represent the three-branch length and two-branch length (evaluated via Equation 9), respectively. B) Alternative four-taxon tree modeled by Siddall [26]. The internode and two subtending branches labeled a’ are constrained to be equal in length (i.e. “alternative three-branch length”), so are the two subtending branches labeled b’ (i.e. “alternative two-branch length”), with p _a ’ and p _b ’ representing the alternative three-branch length and two-branch length, respectively. C) Branch length space of the model tree investigated by Huelsenbeck and Hillis [22], with the three-branch length p _a on the horizontal axis and the two-branch length p _b on the vertical axis. These axes apply to Figures 3A, C, and E. The upper-left portion of this branch length space corresponds to the Felsenstein zone. D) Branch length space of the alternative model tree investigated by Siddall [26], with the alternative three-branch length p _a ’ on the horizontal axis and the alternative two-branch length p _b ’ on the vertical axis. These axes correspond to those in Figures 3B, D, and F. The upper-left portion of this branch length space corresponds to the Farris zone as termed by Siddall [26].

Figure 3

Contour map of y ∕ Max(x ₁, x ₂) for a nucleotide character which assumes the JC model over the branch length space of A) the Huelsenbeck and Hillis [22] model tree and B) the Siddall [26] model tree, with contour lines of y ∕ Max(x ₁, x ₂) = 1/10, 1/6, 1/4, 1/2, 1 (thick dashed), 2, 4, 6, and 10 shown if present within the respective branch length space. Contour map of Π ∕ y for a nucleotide character under the JC model over the branch length space of C) the Huelsenbeck and Hillis [22] model tree and D) the Siddall [26] model tree, with contour lines of Π ∕ y = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 (thick dashed) shown if present. Contour map of Π ∕ Max(x ₁, x ₂) for a nucleotide character under the JC model over the branch length space of E) the Huelsenbeck and Hillis [22] model tree and F) the Siddall [26] model tree, with contour lines of Π ∕ Max(x ₁, x ₂) = 1/10, 1/6, 1/4, 1/2, 1 (thick dashed), 2, 4, 6, and 10 shown if present.

Figure 4

The predicted utility Π − Max(x ₁, x ₂) versus substitution rate λ based on the JC model is plotted for l = 1.5 (solid line), l = 2 (dotted line), l = 2.5 (dashed line), and l = 3 (dot-dashed line), for the four-taxon tree as depicted in Figure 1 in which λ ₀ = λ ₁ = λ ₂ = λ ₃ = λ ₄ = λ, t ₀ = 0.1, T ₁ = T ₃ = 0.4, and T ₂ = T ₄ = 0.4l.

Figure 5

The predicted utility Π − Max(x ₁, x ₂) versus substitution rate λ based on the JC model is plotted for l = 1.5 (solid line), l = 2 (dotted line), l = 2.5 (dashed line), and l = 3 (dot-dashed line), for the four-taxon tree as depicted in Figure 1 in which t ₀ = 0.1, T ₁ = T ₂ = T ₃ = T ₄ = lt ₀, λ ₁ = λ ₃ = 1, and λ ₀ = λ ₂ = λ ₄ = λ.

Figure 6

The predicted utility Π − Max(x ₁, x ₂) versus substitution rate λ is plotted based on the JC [63] model (solid line), the K2P (dotted line), the HKY (dashed line), and the GTR model (dot-dashed line), for the four-taxon tree as depicted in Figure 1 in which t ₀ = 0.1, T ₁ = T ₂ = T ₃ = T ₄ = 0.25, λ ₁ = λ ₃ = 1, and λ ₀ = λ ₂ = λ ₄ = λ. The model parameter values are presented in Table 1.