Maintenance of Quantitative Genetic Variance Under Partial Self-Fertilization, with Implications for Evolution of Selfing

Abstract

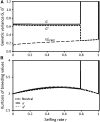
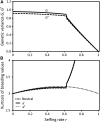
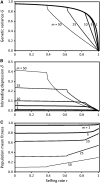
We analyze two models of the maintenance of quantitative genetic variance in a mixed-mating system of self-fertilization and outcrossing. In both models purely additive genetic variance is maintained by mutation and recombination under stabilizing selection on the phenotype of one or more quantitative characters. The Gaussian allele model (GAM) involves a finite number of unlinked loci in an infinitely large population, with a normal distribution of allelic effects at each locus within lineages selfed for τ consecutive generations since their last outcross. The infinitesimal model for partial selfing (IMS) involves an infinite number of loci in a large but finite population, with a normal distribution of breeding values in lineages of selfing age τ. In both models a stable equilibrium genetic variance exists, the outcrossed equilibrium, nearly equal to that under random mating, for all selfing rates, r, up to critical value, [Formula: see text], the purging threshold, which approximately equals the mean fitness under random mating relative to that under complete selfing. In the GAM a second stable equilibrium, the purged equilibrium, exists for any positive selfing rate, with genetic variance less than or equal to that under pure selfing; as r increases above [Formula: see text] the outcrossed equilibrium collapses sharply to the purged equilibrium genetic variance. In the IMS a single stable equilibrium genetic variance exists at each selfing rate; as r increases above [Formula: see text] the equilibrium genetic variance drops sharply and then declines gradually to that maintained under complete selfing. The implications for evolution of selfing rates, and for adaptive evolution and persistence of predominantly selfing species, provide a theoretical basis for the classical view of Stebbins that predominant selfing constitutes an "evolutionary dead end."

Keywords: inbreeding depression; mixed mating; polygenic mutation; purging; stabilizing selection.

Figure 1

Purging of genetic variance under continued selfing in the GAM for each of 25 identical independent characters under stabilizing selection. Components of genetic variance (A and B) and mean fitness (C and D) as functions of selfing age and distribution of selfing ages (E and F) for population selfing rates below ($r=0.78$, A, C, and E) or above ($r=0.8$, B, D, and F) the purging threshold. Note the different scales in A and B. In B the genetic variance G at young selfing ages and genic variance V and covariance C are not at equilibrium; their values depend on the number of generations simulated (here 500,000). In E and F dotted lines represent the distribution of selfing age classes in Wright’s neutral model. Other parameters: $E=1$, ${\sigma }_{\mathrm{m}}^2=0.001$, $n=10$, and ${\omega }^2=20.$

Figure 2

Purging of genetic variance under continued selfing in the IMS for each of 25 identical independent characters under stabilizing selection. Panels and parameters are as in Figure 1 but for the IMS with $V\left(0\right)=1.$ (A and B) Total genetic variance after selection is virtually indistinguishable from that before selection. At selfing rates above the purging threshold, $r>\widehat{r}$, the IMS shows smaller changes in genetic variance and mean fitness as a function of selfing age than the GAM (B and D compared to Figure 1, B and D) but still displays similar patterns of selfing age distribution (E and F compared to Figure 1, E and F).

Figure 3

Equilibrium genetic variance as a function of selfing rate for each of 25 identical uncorrelated characters under stabilizing selection in the GAM. (A) Total genetic variance before and after selection, G and $G*$. (B) Kurtosis of breeding values, κ, before and after selection at the outcrossed equilibrium for r below the purging threshold, at the purged equilibrium for r above the purging threshold, and in Wright’s neutral model. Other parameters are as in Figure 1.

Figure 4

Equilibrium genetic variance as a function of selfing rate for each of 25 identical uncorrelated characters under stabilizing selection in the IMS. (A) Total genetic variance before and after selection. (B) Kurtosis in breeding value, κ, before and after selection, and in Wright’s neutral model. Other parameters are as in Figure 2.

Figure 5

Equilibrium genetic variance after selection (A), inbreeding depression (B), and population mean fitness (C), as functions of population selfing rate, for different numbers of characters in the GAM. When the selfing rate is below the purging threshold, two stable equilibria exist. The outcrossed equilibrium has relatively large genetic variance and inbreeding depression nearly independent of selfing rate (solid lines); it is reached when the population has initially low genetic variance and low linkage equilibrium. The purged equilibrium (dashed lines) has lower genetic variance, independent of the number of characters, and negative inbreeding depression for r just above the purging threshold. Other parameters are as in Figure 1.

Figure 6

Equilibrium genetic variance before selection in the IMS (A), along with inbreeding depression and population mean fitness (B and C), as functions of population selfing rate, for different numbers of characters m. Other parameters are as in Figure 2.

Figure 7

Equilibrium genetic variance before selection in the IMS (A and B), along with inbreeding depression and population mean fitness (C and D), as functions of population selfing rate, for different numbers of characters m with no pleiotropy subject to correlational selection between $m/2$ independent pairs of characters. In the selection matrix (Equation 2) off-diagonal elements for pairs of characters under correlational selection are 0.5 times the diagonal elements (${\omega }^2$). The equilibrium genetic covariance between pairs of characters under correlational selection is caused by linkage disequilibrium, and $B/G$ represents their genetic correlation. Other parameters are as in Figure 2.