QCD and strongly coupled gauge theories: challenges and perspectives
- PMID: 25972760
- PMCID: PMC4413533
- DOI: 10.1140/epjc/s10052-014-2981-5
QCD and strongly coupled gauge theories: challenges and perspectives
Abstract
We highlight the progress, current status, and open challenges of QCD-driven physics, in theory and in experiment. We discuss how the strong interaction is intimately connected to a broad sweep of physical problems, in settings ranging from astrophysics and cosmology to strongly coupled, complex systems in particle and condensed-matter physics, as well as to searches for physics beyond the Standard Model. We also discuss how success in describing the strong interaction impacts other fields, and, in turn, how such subjects can impact studies of the strong interaction. In the course of the work we offer a perspective on the many research streams which flow into and out of QCD, as well as a vision for future developments.
Figures











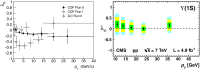


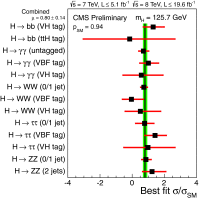
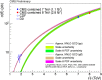
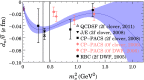

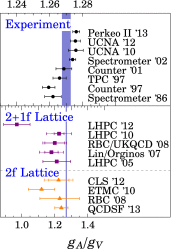
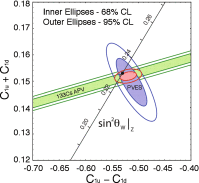
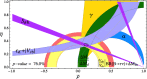







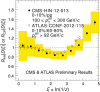


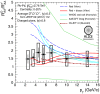
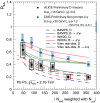
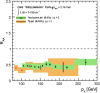


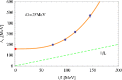
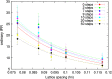
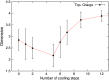

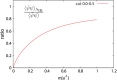





References
-
- J. Beringer et al. (Particle Data Group), Phys. Rev. D 86, 010001 (2012)
-
- McNeile C, Davies CTH, Follana E, Hornbostel K, Lepage GP. Phys. Rev. D. 2010;82:034512. - PubMed
-
- Shintani E, Aoki S, Fukaya H, Hashimoto S, Kaneko T, et al. Phys. Rev. D. 2010;82:074505.
-
- S. Aoki et al. (PACS-CS Collaboration), JHEP 0910, 053 (2009). arXiv:0906.3906
-
- Blossier B, Boucaud P, Brinet M, De Soto F, Du X, et al. Phys. Rev. Lett. 2012;108:262002. - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
