A theoretical study on seasonality

Abstract

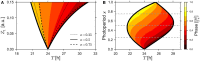
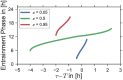
In addition to being endogenous, a circadian system must be able to communicate with the outside world and align its rhythmicity to the environment. As a result of such alignment, external Zeitgebers can entrain the circadian system. Entrainment expresses itself in coinciding periods of the circadian oscillator and the Zeitgeber and a stationary phase difference between them. The range of period mismatches between the circadian system and the Zeitgeber that Zeitgeber can overcome to entrain the oscillator is called an entrainment range. The width of the entrainment range usually increases with increasing Zeitgeber strength, resulting in a wedge-like Arnold tongue. This classical view of entrainment does not account for the effects of photoperiod on entrainment. Zeitgebers with extremely small or large photoperiods are intuitively closer to constant environments than equinoctial Zeitgebers and hence are expected to produce a narrower entrainment range. In this paper, we present theoretical results on entrainment under different photoperiods. We find that in the photoperiod-detuning parameter plane, the entrainment zone is shaped in the form of a skewed onion. The bottom and upper points of the onion are given by the free-running periods in DD and LL, respectively. The widest entrainment range is found near photoperiods of 50%. Within the onion, we calculated the entrainment phase that varies over a range of 12 h. The results of our theoretical study explain the experimentally observed behavior of the entrainment phase in dependence on the photoperiod.

Keywords: circadian clock; entrainment; oscillator; seasonality.

Figure 1

(A) 1:1 synchronization region in the Z₁ − T parameter plane (1:1 Arnold tongue). Dotted, bold, and dashed black lines denote bifurcation curves of periodic solutions as determined by a continuation method for different photoperiods ϰ = 0.25, ϰ = 0.5, and ϰ = 0.75. Phases of the solutions in the 1:1 synchronization regime to equinox photoperiods (i.e., ϰ = 0.5) are color-coded. (B) 1:1 Entrainment range (Arnold onions) and color-coded phases in the ϰ–T-plane given a Zeitgeber strength of Z₁ = 0.1. Dashed lines denote the corresponding photoperiods ϰ = 0.25, ϰ = 0.5, and ϰ = 0.75. Simulations for both Figures relied on the parameters τ = 24 h, λ = 0.5 h⁻¹, and A = 1. The color-coded phases in the entrainment regions were determined by a “brute force integration method” as described in Section 2.3.

Figure 2

(A) Free-running period τ as a function of the intensity Z₁ of a constant forcing signal, i.e., Z(t) = Z₁ for all times t, which is equivalent to setting ϰ to one in Eq. 5. (B) Dependence of the entrainment region on varying intensities Z₁ of a rhythmic Zeitgeber Z(t) as defined by Eq. 5 in Section S1.3 in Supplementary Material. A Zeitgeber steepness of S = 100 was used. Simulations were done for a (uniform) Poincaré oscillator with parameters ε = 0 h⁻¹, A = 1, and λ = 0.5 h⁻¹. A three-dimensional representation of (B) can be found in Figure S3 in Supplementary Material.

Figure 3

(A) Plotted are the Fourier coefficients R_k(ϰ) of order k = 1, 2, 3, 4 from the Fourier decomposition (Eq. 6) of the asymmetric square-wave signal (Eq. 5). (B,C) Entrainment regions in the ϰ − t parameter plane. Gray areas denote these entrainment regions as determined by the “brute force integration method” as described in Section 2.3. Dashed black lines denote the entrainment border for system (Eq. 4), driven by the rectangular Zeitgeber signal Z(t) from Eq. 15 in Section S1.3 in Supplementary Material, using a Zeitgeber steepness of S = 100. Bold colored lines denote the borders of entrainment of the same system (Eq. 4) in case it is driven by the sum of the zeroth and k-th Fourier mode from the Fourier expansion (Eq. 6). Zeitgeber and oscillator properties are given by Z₁ = 0.1, and T = 24 h as well as A = 1, λ = 0.5 h⁻¹, and ε = 0 h⁻¹, respectively.

Figure 4

Entrainment phases ψ as a function of the period mismatch τ − T between the intrinsic oscillator period τ and the Zeitgeber period T for different photoperiods ϰ. The curves correspond to horizontal cross-section of Figure 1B at the ordinate positions ϰ = 0.05, ϰ = 0.5, and ϰ = 0.95, respectively; i.e., the same Zeitgeber intensity Z₁ and oscillator properties ε, A, λ, and τ were used as those underlying the simulations in Figure 1B.

Figure 5

(A) Entrainment regions and color-coded entrainment phases in the ϰ − t parameter plane are plotted for T = 24 h and two different Zeitgeber intensities, namely Z₁ = 0.05 (blue color-map) and Z₁ = 0.1 (red color-map). (B) Entrainment phases ψ as a function of the photoperiod ϰ for different intrinsic periods τ, obtained from the Arnold onion for Z₁ = 0.1. The curves correspond to the vertical cross-sections depicted by dashed gray lines in (A). Other oscillator parameters were A = 1 and λ = 0.5 h⁻¹.