Full correlation matrix analysis (FCMA): An unbiased method for task-related functional connectivity

Abstract

Background: The analysis of brain imaging data often requires simplifying assumptions because exhaustive analyses are computationally intractable. Standard univariate and multivariate analyses of brain activity ignore interactions between regions and analyses of interactions (functional connectivity) reduce the computational challenge by using seed regions of interest or brain parcellations.

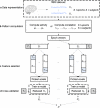
New method: To meet this challenge, we developed full correlation matrix analysis (FCMA), which leverages and optimizes algorithms from parallel computing and machine learning to efficiently analyze the pairwise correlations of all voxels in the brain during different cognitive tasks, with the goal of identifying task-related interactions in an unbiased manner.

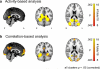
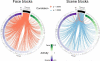
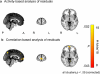
Results: When applied to a localizer dataset on a small compute cluster, FCMA accelerated a naive, serial approach by four orders of magnitude, reducing running time from two years to one hour. In addition to this performance gain, FCMA emphasized different brain areas than existing methods. In particular, beyond replicating known category selectivity in visual cortex, FCMA also revealed a region of medial prefrontal cortex whose selectivity derived from differential patterns of functional connectivity across categories.

Comparison with existing method(s): For benchmarking, we started with a naive approach and progressively built up to the complete FCMA procedure by adding optimized classifier algorithms, multi-threaded parallelism, and multi-node parallelism. To evaluate what can be learned with FCMA, we compared it against multivariate pattern analysis of activity and seed-based analysis of functional connectivity.

Conclusions: FCMA demonstrates how advances in computer science can alleviate computational bottlenecks in neuroscience. We have released a software toolbox to help others evaluate FCMA.

Keywords: Functional magnetic resonance imaging; Machine learning; Multivariate pattern analysis; Parallel computing.

Fig. 1

Workflow overview. FCMA uses a controller/worker architecture, in which each worker first loads the full data into memory. The full data consist of a matrix with V voxels in rows and T timepoints in columns; the timepoints can be subdivided into E epochs, each with T_E timepoints (inset depicts two voxels and epochs). The controller process does the following: assigns a subset S of voxels to each of W workers; instructs the worker to compute the correlation between each of these voxels and the rest of the brain in each epoch; instructs the worker to analyze the correlation vectors for each voxel across epochs with MVPA and supplied condition labels; collects the analysis result (i.e., cross-validation accuracy) for each voxel and loads it into memory; and returns to the first step to assign another subset of voxels until there are none left. Finally, the controller writes the results to disk.

Fig. 2

Classification procedure. (a) The preprocessed fMRI data set contains n subjects, each represented with a k voxels by t epochs matrix. (b) For standard MVPA of activity patterns, vectors are defined for each subject and epoch as the average BOLD signal over time in every voxel (μ_i). For MVPA of correlation patterns, vectors are defined for each subject and epoch as the pairwise correlation of the BOLD signal over time between every voxel and every other voxel (r_i,j). (c) The same nested cross-validation pipeline can be applied to activity and correlation patterns. The inner loop serves to select features (voxels) for classification: A training set (S_i) is divided into m pieces to do an m-fold cross-validation that identifies the voxels with highest performance. (d) The outer loop is n-fold, with each fold leveraging the selected voxels to train a model on S_i and test it on the left-out test set (T_i). This results in a classification accuracy (P_i), which is then averaged across folds (P) to quantify overall performance.

Fig. 3

(a) Activity-based analysis. Sagittal, coronal, and axial sections depicting voxels in which surrounding activity led to reliable classification of object category. These voxels were found in areas of ventral temporal, dorsal occipital, and retrosplenial cortex. (b) Correlation-based analysis. The same sections depicting voxels whose correlations with all other voxels led to reliable classification of object category. These voxels were found in areas overlapping with the activity-based analysis, but also in mPFC, early visual cortex, and precuneus. The color of each voxel reflects the frequency with which it was selected across cross-validation folds. P = posterior, A = anterior, R = right, L = left.

Fig 4

Analysis of mPFC correlation vectors. For each subject and category, a vector of the average correlation between mPFC and each of the 1337 voxels in occipital and temporal cortex was computed. A 2-D projection of these vectors for each subject is depicted in gray, with the average across subjects in color. Each vector pair belonging to the same subject was placed symmetrically around the vertical meridian, and the angle between them was the real angle in the high-dimensional space. The lengths were rendered proportional to the group mean.

Fig. 5

(a) The average correlations of FFA and PPA voxels with mPFC plotted as a function of block type. (b) The average evoked BOLD activity of FFA, PPA, and mPFC voxels plotted as a function of block type. The FFA and PPA voxels were selected as face- and scene-selective, respectively, using a GLM. They were thus guaranteed to show this pattern of activity, which we display here only for visualization purposes.

Fig 6

mPFC correlation patterns for face and scene blocks. Each point on the circle represents a voxel, with mPFC voxels shown in black and visual voxels arranged clockwise according to their activity-based selectivity, from face (green) to scene (purple). Links are drawn for correlations between pairs of voxels that were reliably positive (red) or negative (blue) in a one-sample t-test across subjects. The surrounding histogram reflects the frequency (8-18) with which each voxel was selected across cross-validation folds (as in Fig. 3). Created with the Circos graphical tool (Krzywinski et al., 2009).

Fig. 7

Sagittal, coronal, and axial sections depicting voxels whose (a) surrounding activity patterns in a searchlight, and (b) correlations with all other voxels led to reliable classification of object category in residuals scrubbed of evoked responses. The color of each voxel reflects the frequency with which it was selected over crossvalidation folds. P = posterior, A = anterior, R = right, L = left.