Beyond non-integer Hill coefficients: A novel approach to analyzing binding data, applied to Na+-driven transporters

Abstract

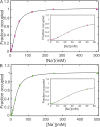
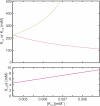
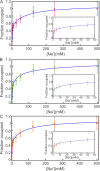
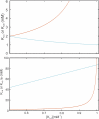
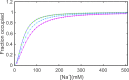
Prokaryotic and eukaryotic Na(+)-driven transporters couple the movement of one or more Na(+) ions down their electrochemical gradient to the active transport of a variety of solutes. When more than one Na(+) is involved, Na(+)-binding data are usually analyzed using the Hill equation with a non-integer exponent n. The results of this analysis are an overall Kd-like constant equal to the concentration of ligand that produces half saturation and n, a measure of cooperativity. This information is usually insufficient to provide the basis for mechanistic models. In the case of transport using two Na(+) ions, an n < 2 indicates that molecules with only one of the two sites occupied are present at low saturation. Here, we propose a new way of analyzing Na(+)-binding data for the case of two Na(+) ions that, by taking into account binding to individual sites, provides far more information than can be obtained by using the Hill equation with a non-integer coefficient: it yields pairs of possible values for the Na(+) affinities of the individual sites that can only vary within narrowly bounded ranges. To illustrate the advantages of the method, we present experimental scintillation proximity assay (SPA) data on binding of Na(+) to the Na(+)/I(-) symporter (NIS). SPA is a method widely used to study the binding of Na(+) to Na(+)-driven transporters. NIS is the key plasma membrane protein that mediates active I(-) transport in the thyroid gland, the first step in the biosynthesis of the thyroid hormones, of which iodine is an essential constituent. NIS activity is electrogenic, with a 2:1 Na(+)/I(-) transport stoichiometry. The formalism proposed here is general and can be used to analyze data on other proteins with two binding sites for the same substrate.

Figure 1.

Binding of a ligand L to a protein P with two cooperative binding sites (sites A and B). The association constants for the empty protein are K_a,A and K_a,B, and those for binding of the second ligand are K_a,A−B and K_a,B−A.

Figure 2.

Na⁺ binding by WT NIS. (A) SPA data for Na⁺ binding by NIS fitted by Eq. 8. Data were collected and analyzed as described in Materials and methods. Values represent the means ± SE from three independent experiments performed in triplicate. The inset shows the fit at low [Na⁺], where the cooperativity is more pronounced. (B) SPA data for Na⁺ binding by WT NIS fitted using the Hill equation with a non-integer coefficient (Eq. 1). The data were fitted with a K_d of 31.8 mM and an n value of 1.74. The inset shows the fit at low [Na⁺], where the cooperativity is more pronounced.

Figure 3.

Ranges of dissociation constants for Na⁺ binding by WT NIS. (Top) Dissociation constants for Na⁺ binding by empty WT NIS—K_d,A (red) and K_d,B (green)—as a function of the allowed values for the association constant K_a,A. (Bottom) Enhanced dissociation constant for the second site when the first site is already occupied.

Figure 4.

Na⁺ binding by S353A/T354A NIS. (A) SPA data for Na⁺ binding by S353A/T354A NIS fitted by Eq. 8. Data were collected and analyzed as described in Materials and methods. Values represent the means ± SE from two independent experiments performed in triplicate. The inset shows the fit at low [Na⁺], where the cooperativity is more pronounced. (B) SPA data for Na⁺ binding by S353A/T354A NIS fitted by the Hill equation with a non-integer coefficient (Eq. 1). The data were fitted with a K_d of 20.6 mM and an n value of 0.42. The inset shows the fit at low [Na⁺], where the cooperativity is more pronounced. (C) SPA data for Na⁺ binding by S353A/T354A NIS fitted for two independent sites. The data were fitted with a K_d,A of 0.90 mM and a K_d,B of 80.5 mM. The inset shows the fit at low [Na⁺], where the effect of having two sites—one with high affinity and one with low affinity—is more pronounced.

Figure 5.

Ranges of dissociation constants for Na⁺ binding by S353A/T354A NIS. (Top) Dissociation constants for Na⁺ binding by empty NIS—K_d,A (cyan) and K_d,B (red)—as a function of the allowed values for the association constant K_a,A. K_d,A = 1/K_a,A varies between 1.98 and 0.99 mM. (Bottom) K_d,B = 1/(K_p − K_a,A) (red) as a function of K_a,A also begins at 1.98 mM (K_p /2; left side of graph) and increases slowly until approximately K_a,A = 0.8 mM⁻¹. As K_a,A approaches K_p, K_a,B approaches infinity (bottom graph, right). In contrast, although K_d,B/ϕ (cyan) begins at 43.78 mM when site A is occupied (negative cooperativity), it only increases to 87.68 mM when K_a,A = K_p (right side of graph).

Figure 6.

Fitting by Eq. 8 of points generated by Eq. 1. Points were generated using Eq. 1 with n values of 1.7 (mauve ovals), 1.8 (blue triangles), and 1.9 (green squares), and a K_dⁿ of 1,000 (K_aⁿ = 0.001). Each set of points was fitted using Eq. 8, resulting in the mauve, cyan, and blue curves, respectively.