The Hill analysis and co-ion-driven transporter kinetics
- PMID: 26009547
- PMCID: PMC4442790
- DOI: 10.1085/jgp.201411332
The Hill analysis and co-ion-driven transporter kinetics
Abstract
Interaction of multiple ligands with a protein or protein complex is a widespread phenomenon that allows for cooperativity. Here, we review the use of the Hill equation, which is commonly used to analyze binding or kinetic data, to analyze the kinetics of ion-coupled transporters and show how the mechanism of transport affects the Hill coefficient. Importantly, the Hill analysis of ion-coupled transporters can provide the exact number of transported co-ions, regardless of the extent of the cooperativity in ion binding.
© 2015 Lolkema and Slotboom.
Figures

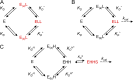
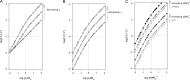
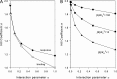
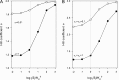
References
-
- Bezanilla F. 2000. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 80:555–592. - PubMed
Publication types
MeSH terms
Substances
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

