Algorithmic lattice kirigami: A route to pluripotent materials

Abstract

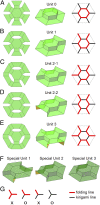
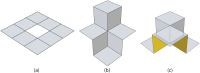
We use a regular arrangement of kirigami elements to demonstrate an inverse design paradigm for folding a flat surface into complex target configurations. We first present a scheme using arrays of disclination defect pairs on the dual to the honeycomb lattice; by arranging these defect pairs properly with respect to each other and choosing an appropriate fold pattern a target stepped surface can be designed. We then present a more general method that specifies a fixed lattice of kirigami cuts to be performed on a flat sheet. This single pluripotent lattice of cuts permits a wide variety of target surfaces to be programmed into the sheet by varying the folding directions.

Keywords: origami; pluripotent; topological defects.

Fig. 1.

Construction and configuration of the fundamental $\tilde{5}$–$\tilde{7}$ climb pair kirigami element. (A) The cut surface in its unfolded state with and without the underlying honeycomb lattice. Because they share an edge after assembly, regions marked “R” must be at the same height in the folded configuration. Regions marked “P” can either be at the same height or differ in height by two. (B–E) The four allowed folding configurations of the $\tilde{5}$–$\tilde{7}$ climb pair element.

Fig. 2.

(A–E) The basic building blocks of $\tilde{5}$–$\tilde{7}$ stepped surfaces. (Left) The unfolded configuration, where the excised hexagons sit on a larger-scale honeycomb lattice. (Middle) The folded configuration. (Right) A reduced representation suitable for easily designing target surfaces. (F) Folded configurations where the positive-climb paths of three dislocations converge. (G) Junction representation of the meeting of folding lines and cutting lines (i.e., places where excised regions had their edges identified) in the reduced representation. Only the junctions marked “O” represent allowed configurations.

Fig. 3.

(A) A triangular lattice of sixons together with lines for mountain (dot-dashed) and valley (dashed) folds to create the ground state configuration. (B) The ground state of the pattern in A, with sidewall heights reduced for visual clarity. (C) A reduced triangular representation for an arbitrary height configuration of the lattice, where the numbers inside each triangle correspond to the height of that triangular plateau. Each plateau height differs by one from any plateau with which it shares an edge. (D) The cut-and-fold pattern corresponding to the height map in C, where the gray hexagons are the excised regions.

Fig. 4.

Illustration of the pluripotent design capability of the sixon lattice. Starting from the base configuration of a 151 × 151 grid of triangular plateaus, a target surface is first selected [here a monkey saddle or Mt. Katahdin (18)]. The height of this target surface is projected onto the grid of triangular patches, and from this a local sequence of fold assignments is made to construct the final kirigami structure.

Fig. S1.

(Top) A duopotent lattice of sixons in the flat state, where gray hexagons denote the excised regions of the paper. Folding the red lines (surrounding the red, upward facing triangles) leads to a Mexican hat potential, whereas folding the blue lines (surrounding the blue, downward facing triangles) leads to a half-cylinder. Dashed lines indicate valley folds, and dash-dotted lines indicate mountain folds. (Bottom) The two folded state configurations of the duopotent sheet.

Fig. S2.

The $\tilde{5}$–$\tilde{7}$ climb pair design of a ziggurat. (A) The target surface. (B) Projecting the integer heights of the target surface down onto a plane decorated with the honeycomb superlattice. As in the main text, red lines indicate folds, and black lines indicate cuts, whereas the numbers indicate the height of the labeled hexagonal plateau. (C) Cut-and-fold pattern corresponding to the projected pattern. (D and E) Computer renderings of the final, folded state.

Fig. S3.

Ziggurat kirigami constructed from Tyvek and polyolefin (video of this structure self-folding at 3× speed available at https://dl.dropboxusercontent.com/u/28290913/zigguratkirigami.mp4).

Fig. S4.

The base unit of square lattice kirigami. The part enclosed by dotted lines is used to tile the plane, and the colors encode the ultimate fate of each square patch in the folded configuration.

Fig. S5.

Construction and configurations of the fundamental square lattice kirigami element. (A) The square lattice defect in its unfolded state. (B and C) Two folded configurations of this element, which capture the allowed states up to rotations.

Fig. S6.

Reduced representation of the square lattice kirigami building blocks. Target configurations can be formed by overlapping these six units (up to addition of a constant integer to each of the four square heights).