Selective buckling via states of self-stress in topological metamaterials
- PMID: 26056303
- PMCID: PMC4485125
- DOI: 10.1073/pnas.1502939112
Selective buckling via states of self-stress in topological metamaterials
Abstract
States of self-stress--tensions and compressions of structural elements that result in zero net forces--play an important role in determining the load-bearing ability of structures ranging from bridges to metamaterials with tunable mechanical properties. We exploit a class of recently introduced states of self-stress analogous to topological quantum states to sculpt localized buckling regions in the interior of periodic cellular metamaterials. Although the topological states of self-stress arise in the linear response of an idealized mechanical frame of harmonic springs connected by freely hinged joints, they leave a distinct signature in the nonlinear buckling behavior of a cellular material built out of elastic beams with rigid joints. The salient feature of these localized buckling regions is that they are indistinguishable from their surroundings as far as material parameters or connectivity of their constituent elements are concerned. Furthermore, they are robust against a wide range of structural perturbations. We demonstrate the effectiveness of this topological design through analytical and numerical calculations as well as buckling experiments performed on two- and three-dimensional metamaterials built out of stacked kagome lattices.
Keywords: isostatic lattices; topological mechanics; topological modes; tunable failure.
Conflict of interest statement
The authors declare no conflict of interest.
Figures
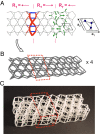
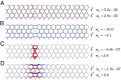


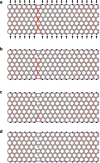
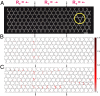


References
-
- Lakes R. Foam structures with a negative Poisson’s ratio. Science. 1987;235(4792):1038–1040. - PubMed
-
- Kadic M, Buckmann T, Stenger N, Thiel M, Wegener M. On the practicability of pentamode mechanical metamaterials. Appl Phys Lett. 2012;100:191901.
-
- Shim J, et al. Harnessing instabilities for design of soft reconfigurable auxetic/chiral materials. Soft Matter. 2013;9:8198–8202.
-
- Babaee S, et al. 2013. 3D soft metamaterials with negative Poisson’s ratio. Adv Mater 25(36):5044–5049.
-
- Shan S, et al. Harnessing multiple folding mechanisms in soft periodic structures for tunable control of elastic waves. Adv Funct Mater. 2014;24(31):4935–4942.
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources

