An investigation of the false discovery rate and the misinterpretation of p-values
- PMID: 26064558
- PMCID: PMC4448847
- DOI: 10.1098/rsos.140216
An investigation of the false discovery rate and the misinterpretation of p-values
Abstract
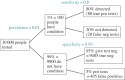
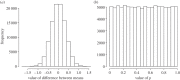
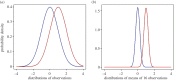
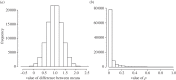
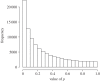
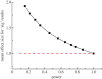
If you use p=0.05 to suggest that you have made a discovery, you will be wrong at least 30% of the time. If, as is often the case, experiments are underpowered, you will be wrong most of the time. This conclusion is demonstrated from several points of view. First, tree diagrams which show the close analogy with the screening test problem. Similar conclusions are drawn by repeated simulations of t-tests. These mimic what is done in real life, which makes the results more persuasive. The simulation method is used also to evaluate the extent to which effect sizes are over-estimated, especially in underpowered experiments. A script is supplied to allow the reader to do simulations themselves, with numbers appropriate for their own work. It is concluded that if you wish to keep your false discovery rate below 5%, you need to use a three-sigma rule, or to insist on p≤0.001. And never use the word 'significant'.
Keywords: false discovery rate; reproducibility; significance tests; statistics.
Figures

References
-
- Sellke T, Bayarri MJ, Berger JO. 2001. Calibration of p values for testing precise null hypotheses. Am. Stat. 55, 62–71. (doi:10.1198/000313001300339950) - DOI
-
- Ioannidis JP. 2005. Why most published research findings are false. PLoS Med. 2, e124 (doi:10.1371/journal.pmed.0020124) - DOI - PMC - PubMed
-
- Colquhoun D. Lectures on biostatistics. (http://www.dcscience.net/Lectures_on_biostatistics-ocr4.pdf)
-
- Scharre DW, Chang SI, Nagaraja HN, Yager-Schweller J, Murden RA. 2014. Community cognitive screening using the self-administered gerocognitive examination (SAGE). J. Neuropsychiatry Clin. Neurosci. 26, 369–375. (doi:10.1176/appi.neuropsych.13060145) - DOI - PubMed
-
- McCartney M. 2013. Would doctors routinely asking older patients about their memory improve dementia outcomes?: No. Br. Med. J. 346, 1745 (doi:10.1136/bmj.f1745) - DOI - PubMed
Publication types
LinkOut - more resources
Full Text Sources
Other Literature Sources
