Multi-level block permutation
- PMID: 26074200
- PMCID: PMC4644991
- DOI: 10.1016/j.neuroimage.2015.05.092
Multi-level block permutation
Abstract
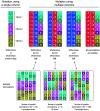
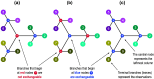
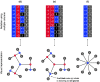
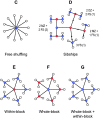
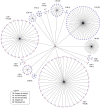
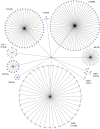
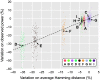
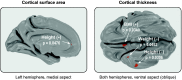
Under weak and reasonable assumptions, mainly that data are exchangeable under the null hypothesis, permutation tests can provide exact control of false positives and allow the use of various non-standard statistics. There are, however, various common examples in which global exchangeability can be violated, including paired tests, tests that involve repeated measurements, tests in which subjects are relatives (members of pedigrees) - any dataset with known dependence among observations. In these cases, some permutations, if performed, would create data that would not possess the original dependence structure, and thus, should not be used to construct the reference (null) distribution. To allow permutation inference in such cases, we test the null hypothesis using only a subset of all otherwise possible permutations, i.e., using only the rearrangements of the data that respect exchangeability, thus retaining the original joint distribution unaltered. In a previous study, we defined exchangeability for blocks of data, as opposed to each datum individually, then allowing permutations to happen within block, or the blocks as a whole to be permuted. Here we extend that notion to allow blocks to be nested, in a hierarchical, multi-level definition. We do not explicitly model the degree of dependence between observations, only the lack of independence; the dependence is implicitly accounted for by the hierarchy and by the permutation scheme. The strategy is compatible with heteroscedasticity and variance groups, and can be used with permutations, sign flippings, or both combined. We evaluate the method for various dependence structures, apply it to real data from the Human Connectome Project (HCP) as an example application, show that false positives can be avoided in such cases, and provide a software implementation of the proposed approach.
Keywords: General linear model; Multiple regression; Permutation inference; Repeated measurements.
Copyright © 2015 The Authors. Published by Elsevier Inc. All rights reserved.
Figures


References
-
- Anderson M.J., Legendre P. An empirical comparison of permutation methods for tests of partial regression coefficients in a linear model. J. Stat. Comput. Simul. 1999;62(3):271–303.
-
- Barch D.M., Burgess G.C., Harms M.P., Petersen S.E., Schlaggar B.L., Corbetta M., Glasser M.F., Curtiss S., Dixit S., Feldt C., Nolan D., Bryant E., Hartley T., Footer O., Bjork J.M., Poldrack R., Smith S., Johansen-Berg H., Snyder A.Z., Van Essen D.C. Function in the human connectome: task-fMRI and individual differences in behavior. NeuroImage. 2013;80:169–189. - PMC - PubMed
-
- Bland J.M., Altman D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;327(8476):307–310. - PubMed
-
- Bond D.J., Ha T.H., Lang D.J., Su W., Torres I.J., Honer W.G., Lam R.W., Yatham L.N. Body mass index-related regional gray and white matter volume reductions in first-episode mania patients. Biol. Psychiatry. 2014;76(2):138–145. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources
Medical
Miscellaneous

