A neural network that finds a naturalistic solution for the production of muscle activity
- PMID: 26075643
- PMCID: PMC5113297
- DOI: 10.1038/nn.4042
A neural network that finds a naturalistic solution for the production of muscle activity
Abstract
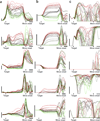
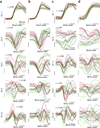
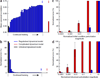
It remains an open question how neural responses in motor cortex relate to movement. We explored the hypothesis that motor cortex reflects dynamics appropriate for generating temporally patterned outgoing commands. To formalize this hypothesis, we trained recurrent neural networks to reproduce the muscle activity of reaching monkeys. Models had to infer dynamics that could transform simple inputs into temporally and spatially complex patterns of muscle activity. Analysis of trained models revealed that the natural dynamical solution was a low-dimensional oscillator that generated the necessary multiphasic commands. This solution closely resembled, at both the single-neuron and population levels, what was observed in neural recordings from the same monkeys. Notably, data and simulations agreed only when models were optimized to find simple solutions. An appealing interpretation is that the empirically observed dynamics of motor cortex may reflect a simple solution to the problem of generating temporally patterned descending commands.
Figures
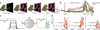




References
-
- Evarts EV. Relation of pyramidal tract activity to force exerted during voluntary movement. J. Neurophysiol. 1968;31:14–27. - PubMed
-
- Mussa-Ivaldi FA. Do neurons in the motor cortex encode movement direction? An alternative hypothesis. Neurosci. Lett. 1988;91:106–111. - PubMed
-
- Sanger TD. Theoretical considerations for the analysis of population coding in motor cortex. Neural Comput. 1994;6:29–37.
-
- Todorov E. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat. Neurosci. 2000;3:391–398. - PubMed
-
- Hatsopoulos NG. Encoding in the motor cortex: was evarts right after all? Focus on ‘motor cortex neural correlates of output kinematics and kinetics during isometric-force and arm-reaching tasks’. J. Neurophysiol. 2005;94:2261–2262. - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

