Network-timing-dependent plasticity
- PMID: 26106298
- PMCID: PMC4460533
- DOI: 10.3389/fncel.2015.00220
Network-timing-dependent plasticity
Abstract
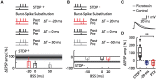
Bursts of activity in networks of neurons are thought to convey salient information and drive synaptic plasticity. Here we report that network bursts also exert a profound effect on Spike-Timing-Dependent Plasticity (STDP). In acute slices of juvenile rat somatosensory cortex we paired a network burst, which alone induced long-term depression (LTD), with STDP-induced long-term potentiation (LTP) and LTD. We observed that STDP-induced LTP was either unaffected, blocked or flipped into LTD by the network burst, and that STDP-induced LTD was either saturated or flipped into LTP, depending on the relative timing of the network burst with respect to spike coincidences of the STDP event. We hypothesized that network bursts flip STDP-induced LTP to LTD by depleting resources needed for LTP and therefore developed a resource-dependent STDP learning rule. In a model neural network under the influence of the proposed resource-dependent STDP rule, we found that excitatory synaptic coupling was homeostatically regulated to produce power law distributed burst amplitudes reflecting self-organized criticality, a state that ensures optimal information coding.
Keywords: STDP; acute brain slices; neural networks simulations; patch-clamp; self-organized criticality; somatosensory cortex; synaptic plasticity.
Figures
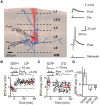

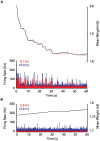
 is the mean excitatory coupling,
is the mean excitatory coupling,  e and
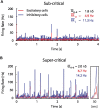
e and  i are the mean firing rate of excitatory (red) and inhibitory (blue) cells in the network, respectively. The simulated network changes its state from sub-critical (A), to super-critical (spontaneous periodic bursting, B) after a 10% increase of mean synaptic weight for excitatory–excitatory connections. (Inset) Example of a typical network burst is shown to the right.
i are the mean firing rate of excitatory (red) and inhibitory (blue) cells in the network, respectively. The simulated network changes its state from sub-critical (A), to super-critical (spontaneous periodic bursting, B) after a 10% increase of mean synaptic weight for excitatory–excitatory connections. (Inset) Example of a typical network burst is shown to the right.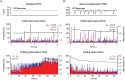
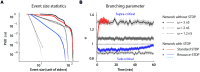
 ) results in different activity regimes: sub-critical with rare aperiodic network bursts (light gray, ω = 1.2 nS), weakly supra-critical with periodic network bursts at rates around 1–10 Hz (dark gray, ω = 2 nS) or strongly supra-critical with periodic network bursts at high rates (black, ω = 3 nS). A standard STDP rule drives the network to a strongly super-critical regime (red), whereas for resource-dependent STDP the resulting burst amplitude statistics follow a power-law (blue). Dashed lines show power-law fits to respective datasets (dot-dashed, ω = 1.2 nS; dashed, ω = 2 nS; cyan-dashed, resource-STDP). (B) The branching parameter (σ) is shown for all networks in (a). In networks without STDP, σ does not evolve (gray traces, ω = 1.2, 2, and 3 nS). With a standard STDP rule, σ increases as the network becomes super-critical (red), whereas with the resource-dependent STDP rule a transition from supra-critical to (sub-) critical occurs rapidly and σ further converges toward a value around 1 (blue).
) results in different activity regimes: sub-critical with rare aperiodic network bursts (light gray, ω = 1.2 nS), weakly supra-critical with periodic network bursts at rates around 1–10 Hz (dark gray, ω = 2 nS) or strongly supra-critical with periodic network bursts at high rates (black, ω = 3 nS). A standard STDP rule drives the network to a strongly super-critical regime (red), whereas for resource-dependent STDP the resulting burst amplitude statistics follow a power-law (blue). Dashed lines show power-law fits to respective datasets (dot-dashed, ω = 1.2 nS; dashed, ω = 2 nS; cyan-dashed, resource-STDP). (B) The branching parameter (σ) is shown for all networks in (a). In networks without STDP, σ does not evolve (gray traces, ω = 1.2, 2, and 3 nS). With a standard STDP rule, σ increases as the network becomes super-critical (red), whereas with the resource-dependent STDP rule a transition from supra-critical to (sub-) critical occurs rapidly and σ further converges toward a value around 1 (blue).References
LinkOut - more resources
Full Text Sources
Other Literature Sources

