Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2015 Jul 6;10(7):e0120644.
doi: 10.1371/journal.pone.0120644. eCollection 2015.

Replication and Analysis of Ebbinghaus' Forgetting Curve

Jaap M J Murre  1 , Joeri Dros  1
Affiliations

Replication and Analysis of Ebbinghaus' Forgetting Curve

Jaap M J Murre et al. PLoS One. .

Abstract

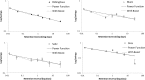
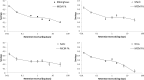
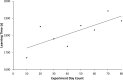
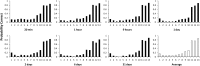
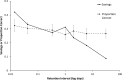
We present a successful replication of Ebbinghaus' classic forgetting curve from 1880 based on the method of savings. One subject spent 70 hours learning lists and relearning them after 20 min, 1 hour, 9 hours, 1 day, 2 days, or 31 days. The results are similar to Ebbinghaus' original data. We analyze the effects of serial position on forgetting and investigate what mathematical equations present a good fit to the Ebbinghaus forgetting curve and its replications. We conclude that the Ebbinghaus forgetting curve has indeed been replicated and that it is not completely smooth but most probably shows a jump upwards starting at the 24 hour data point.

PubMed Disclaimer

Conflict of interest statement

Competing Interests: The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Learning schedule during 2011–2012 for all lists, where labels in bold indicate when each of the lists 1 to 10 was first learned for each retention interval.
Relearning times are not shown but can be derived by adding the retention interval (e.g., 6 days).
Fig 2
Fig 2. Four loglog graphs with savings as a function of retention interval with fitted power function curves and curves with best fitting power functions with boost at 1 day (see text for an explanation).
Fig 3
Fig 3. Four log graphs with savings as a function of retention interval with best-fitting Memory Chain Model retention functions (see text for an explanation).
Fig 4
Fig 4. Normalized savings scores as a function of retention interval on a logarithmic scale, rescaled so the first data point is 1.0 for all curves.
Fig 5
Fig 5. Learning time per list as a function of day of experiment with a fitted straight line.
Fig 6
Fig 6. Serial position for correct relearning scores for each retention interval and for the average of all retention intervals (see text for an explanation).
Fig 7
Fig 7. Proportion correct as a function of retention interval on a logarithmic scale.
(a) Proportion correct, averaged over all serial positions, shown with Dros’ savings scores for comparison. (b) Proportion correct curves for different groups of serial positions and for the average over all 13 positions.
See this image and copyright information in PMC

References

    1. Anderson JR, Schooler LJ (1991) Reflections of the environment in memory. Psychological Science 2: 396–408.
    1. Rubin DC, Wenzel AE (1996) One hundred years of forgetting: A quantitative description of retention. Psychological Review 103: 734–760.
    1. Wixted JT, Carpenter SK (2007) The Wickelgren Power Law and the Ebbinghaus Savings Function. Psychological Science 18: 133–134. - PubMed
    1. Wixted JT, Ebbesen EB (1991) On the form of forgetting. Psychological Science 2: 409–415.
    1. Bartlett FC (1932) Rembering. Cambridge: Cambridge University Press.