Non-straight cell edges are important to invasion and engulfment as demonstrated by cell mechanics model

Abstract

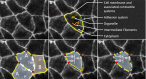
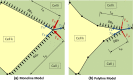
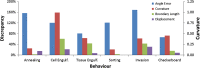
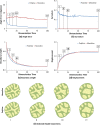
Computational models of cell-cell mechanical interactions typically simulate sorting and certain other motions well, but as demands on these models continue to grow, discrepancies between the cell shapes, contact angles and behaviours they predict and those that occur in real cells have come under increased scrutiny. To investigate whether these discrepancies are a direct result of the straight cell-cell edges generally assumed in these models, we developed a finite element model that approximates cell boundaries using polylines with an arbitrary number of segments. We then compared the predictions of otherwise identical polyline and monoline (straight-edge) models in a variety of scenarios, including annealing, single- and multi-cell engulfment, sorting, and two forms of mixing--invasion and checkerboard pattern formation. Keeping cell-cell edges straight influences cell motion, cell shape, contact angle, and boundary length, especially in cases where one cell type is pulled between or around cells of a different type, as in engulfment or invasion. These differences arise because monoline cells have restricted deformation modes. Polyline cells do not face these restrictions, and with as few as three segments per edge yielded realistic edge shapes and contact angle errors one-tenth of those produced by monoline models, making them considerably more suitable for situations where angles and shapes matter, such as validation of cellular force-inference techniques. The findings suggest that non-straight cell edges are important both in modelling and in nature.

Keywords: Cell engulfment; Cell mechanics; Cell mixing; Cell sorting; Cell–cell interactions; Checkerboard patterns; Computational modelling; Computer simulations; Finite element models; Invasion; Polyline models; Tissue engulfment.

Fig. 1

An epithelium and its corresponding models. a An image of amnioserosa cells in a Drosophila embryo during early dorsal closure (courtesy of M. Shane Hutson). Primary functional and force-generating structures are shown in (b). c Illustrates the net interfacial tensions $\mathrm{\gamma }$ acting along the cell boundaries and the effective viscosity $\mathrm{\mu }$ of their cytoplasm. For explanatory purposes only, the cells are considered to be of two types and the tensions associated with different kinds of boundaries are labelled with subscripts. d Monoline model of the system in (c) and straight rod elements (shown in yellow) are used to represent each cell edge and to carry its interfacial tension $\mathrm{\gamma }$. Select dashpots representing the effective cytoplasm viscosity $\mathrm{\mu }$ are shown. Notice that nodes (red dots) exist only at the triple (or higher-order) junctions. e The associated polyline model and its segmented edges have multiple rod elements connected by intermediate nodes (shown in blue). Note how the segmented edges much more closely approximate the true cell shapes

Fig. 2

How monoline edges restrict motion. The edge tensions in the figure were chosen so that they should pull the yellow cell between the two green cells (Brodland 2002), though the lengths of the tension vectors do not reflect their relative magnitudes. However, when cell edges are forced to remain straight, as in (a), intracellular pressure differences $\mathrm{\Delta }{\text{p}}_{\mathrm{ab}}$ can act over a long enough length ${\text{L}}_{\mathrm{ab}}$ that the equivalent shear forces ${\text{V}}_{\mathrm{ab}}$ they generate (Eq. 2) and transmit to the triple junction (in this case between cells i, j and k) can prematurely arrest its motion. When a polyline model is used (b), the segment lengths ${\text{L}}_{\mathrm{ab}}$ are shorter and the resulting shear forces have a much reduced effect

Fig. 3

A comparison of monoline and polyline models. The models are compared in terms of angle error, curvature, boundary length and displacement for each cell interaction scenario. Details of the calculations are given in the text and may vary from one scenario to the next, depending on the particular features of interest. All values are reported as percentage differences between the monoline and polyline models (left ordinate), except for curvature (right ordinate)

Fig. 4

A closer look at cell sorting and engulfment. a How median RMS angle error (see text) changes with dimensionless time (Brodland et al. 2006). b The average absolute value of edge curvature normalized to a circle of the same area as the average cell. c The total length of the yellow–green boundary normalized to its initial length. d Displacement (see text for details) normalized to cell diameter. e The geometries of the aggregates corresponding to the Roman numerals on the graphs

Fig. 5

A closer look at invasion. As in Fig. 4, a shows median RMS angle error, b gives edge curvature, c reports the normalized total length of the yellow–green boundary and d shows the normalized horizontal displacement. e The geometries corresponding to the Roman numerals on the graphs