A structural model for the in vivo human cornea including collagen-swelling interaction
- PMID: 26156299
- PMCID: PMC4535401
- DOI: 10.1098/rsif.2015.0241
A structural model for the in vivo human cornea including collagen-swelling interaction
Abstract
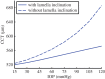
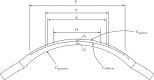
A structural model of the in vivo cornea, which accounts for tissue swelling behaviour, for the three-dimensional organization of stromal fibres and for collagen-swelling interaction, is proposed. Modelled as a binary electrolyte gel in thermodynamic equilibrium, the stromal electrostatic free energy is based on the mean-field approximation. To account for active endothelial ionic transport in the in vivo cornea, which modulates osmotic pressure and hydration, stromal mobile ions are shown to satisfy a modified Boltzmann distribution. The elasticity of the stromal collagen network is modelled based on three-dimensional collagen orientation probability distributions for every point in the stroma obtained by synthesizing X-ray diffraction data for azimuthal angle distributions and second harmonic-generated image processing for inclination angle distributions. The model is implemented in a finite-element framework and employed to predict free and confined swelling of stroma in an ionic bath. For the in vivo cornea, the model is used to predict corneal swelling due to increasing intraocular pressure (IOP) and is adapted to model swelling in Fuchs' corneal dystrophy. The biomechanical response of the in vivo cornea to a typical LASIK surgery for myopia is analysed, including tissue fluid pressure and swelling responses. The model provides a new interpretation of the corneal active hydration control (pump-leak) mechanism based on osmotic pressure modulation. The results also illustrate the structural necessity of fibre inclination in stabilizing the corneal refractive surface with respect to changes in tissue hydration and IOP.
Keywords: collagen-swelling interaction; cornea; hydration; osmotic pressure; proteoglycan; pump-leak.
© 2015 The Author(s).
Figures
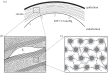
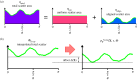
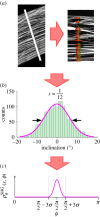
 (Online version in colour.)
(Online version in colour.)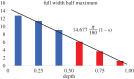
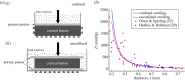
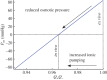
 The swelling pressure data have been extracted from the original papers by free graphics software P
The swelling pressure data have been extracted from the original papers by free graphics software P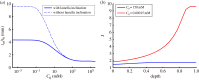
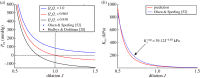
 which is computed by the power law fit function for swelling pressure
which is computed by the power law fit function for swelling pressure  from [52]. (Online version in colour.)
from [52]. (Online version in colour.)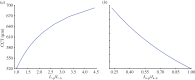
 ) with normal active ionic flux (
) with normal active ionic flux ( ) and (b) the active ionic flux rate is reduced up to a factor of 0.2 (
) and (b) the active ionic flux rate is reduced up to a factor of 0.2 ( ) with normal anionic permeability (
) with normal anionic permeability ( ). (Online version in colour.)
). (Online version in colour.)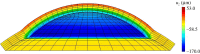
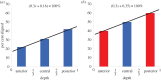
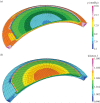
 for a cornea with Fuchs' dystrophy. The anterior surface of the cornea deforms much less than that of the posterior surface. It is noted that the sclera elements are distorted at the limbus. This artefact is due to the abrupt transition from swelling to non-swelling tissue, and may be removed by defining a transition zone between the cornea and sclera.
for a cornea with Fuchs' dystrophy. The anterior surface of the cornea deforms much less than that of the posterior surface. It is noted that the sclera elements are distorted at the limbus. This artefact is due to the abrupt transition from swelling to non-swelling tissue, and may be removed by defining a transition zone between the cornea and sclera.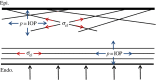
References
-
- Elliott GF, Hodson SA. 1998. Cornea, and the swelling of polyelectrolyte gels of biological interest. Rep. Prog. Phys. 61, 1325–1365. (10.1088/0034-4885/61/10/001) - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources
