Frequency-domain order parameters for the burst and spike synchronization transitions of bursting neurons

Abstract

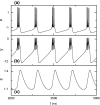
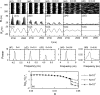
We are interested in characterization of synchronization transitions of bursting neurons in the frequency domain. Instantaneous population firing rate (IPFR) [Formula: see text], which is directly obtained from the raster plot of neural spikes, is often used as a realistic collective quantity describing population activities in both the computational and the experimental neuroscience. For the case of spiking neurons, a realistic time-domain order parameter, based on [Formula: see text], was introduced in our recent work to characterize the spike synchronization transition. Unlike the case of spiking neurons, the IPFR [Formula: see text] of bursting neurons exhibits population behaviors with both the slow bursting and the fast spiking timescales. For our aim, we decompose the IPFR [Formula: see text] into the instantaneous population bursting rate [Formula: see text] (describing the bursting behavior) and the instantaneous population spike rate [Formula: see text] (describing the spiking behavior) via frequency filtering, and extend the realistic order parameter to the case of bursting neurons. Thus, we develop the frequency-domain bursting and spiking order parameters which are just the bursting and spiking "coherence factors" [Formula: see text] and [Formula: see text] of the bursting and spiking peaks in the power spectral densities of [Formula: see text] and [Formula: see text] (i.e., "signal to noise" ratio of the spectral peak height and its relative width). Through calculation of [Formula: see text] and [Formula: see text], we obtain the bursting and spiking thresholds beyond which the burst and spike synchronizations break up, respectively. Consequently, it is shown in explicit examples that the frequency-domain bursting and spiking order parameters may be usefully used for characterization of the bursting and the spiking transitions, respectively.

Keywords: Burst and spike synchronization transitions; Bursting neurons; Frequency-domain order parameters.

Fig. 1

Single HR neuron for $I_{DC}=1.3$ and $D=0$. Plots of time series of a the fast membrane potential $x(t)$, b the fast recovery current $y(t)$, and c the slow adaptation current $z(t)$

Fig. 2

Population bursting states for various values of $D$ and determination of the bursting noise threshold $D_b^{\ast }$ in an inhibitory ensemble of $N$ globally-coupled bursting HR neurons for $I_{DC}=1.3$ and $J=0.3$: synchronized bursting states for $D=0,$ 0.01, 0.04, and 0.06, and unsynchronized bursting state for $D=0.08$. $N={10}^3$ except for the case of (e). a1–a5 Raster plots of neural spikes, b1–b5 time series of IPFR kernel estimate $R(t)$ (the band width $h$ of the Gaussian kernel function is 1 ms), c1–c5 time series of band-pass filtered IPBR $R_b(t)$ [lower and higher cut-off frequencies of 3 Hz (high-pass filter) and 7 Hz (low-pass filter)], and d1–d5 one-sided power spectra of $\mathit{\Delta }{R}_b(t)[=R_b(t)-\overline{R_b(t)}]$ with mean-squared amplitude normalization. Each power spectrum in d1–d5 is made of $2^{15}$ data points and it is smoothed by the Daniell filters of lengths 3 and 5. e Plots of realistic frequency-domain bursting order parameter ${⟨{\mathit{\beta }}_b⟩}_r$ versus $D$:${⟨{\mathit{\beta }}_b⟩}_r$ is obtained through average over 20 realizations for each $D$

Fig. 3

Population intraburst spiking states for various values of $D$ and determination of the bursting noise threshold $D_s^{\ast }$ in an inhibitory ensemble of $N$ globally-coupled bursting HR neurons for $I_{DC}=1.3$ and $J=0.3$: synchronized spiking states for $D=0,$ 0.005, 0.01, and 0.02, and unsynchronized spiking state for $D=0.06$. $N={10}^3$ except for the case of (d). a1–a5 Raster plots of neural spikes and b1–b5 time series of the band-pass filtered IPSR $R(t)$ [lower and higher cut-off frequencies of 30 Hz (high-pass filter) and 90 Hz (low-pass filter)] in the 1st global bursting cycle of the IPBR $R_b(t)$ (after the transient time of $2\times {10}^3$ ms) for each $D$. c1–c5 One-sided power spectra of $\mathit{\Delta }{R}_s(t)[=R_s(t)-\overline{R_s(t)}]$ with mean-squared amplitude normalization. Each power spectrum in c1–c5 is made of $2^8$ data points for each global bursting cycle of $R_b(t)$ and it is smoothed by the Daniell filters of lengths 3 and 5. d Plots of realistic frequency-domain spiking order parameter ${⟨{⟨{\mathit{\beta }}_s⟩}_b⟩}_r$ versus $D$; ${⟨{⟨{\mathit{\beta }}_s⟩}_b⟩}_r$ is obtained through double-averaging over the 20 bursting cycles and the 20 realizations

Fig. 4

Population bursting states represented by the bursting onset and offset times for various values of $D$ and determination of the bursting noise threshold $D_b^{\ast }$ in an inhibitory ensemble of $N$ globally-coupled bursting HR neurons for $I_{DC}=1.3$ and $J=0.3$: synchronized bursting states for $D=0,$ 0.01, 0.04, and 0.06, and unsynchronized bursting state for $D=0.08$. $N={10}^3$ except for the cases of (g1) and (g2). a1–a5 Raster plots of the bursting onset times and b1–b5 time series of the IPBR $R_b^{(on)}(t)$ (the band width $h$ of the Gaussian kernel function is 50 ms). c1–c5 Raster plot of the bursting offset times and d1–d5 time series of the IPBR $R_b^{(off)}(t)$ (the band width $h$ of the Gaussian kernel function is 50 ms). e1–e5 One-sided power spectra of $\mathit{\Delta }{R}_b^{(on)}(t)[=R_b^{(on)}(t)-\overline{R_b^{(on)}(t)}]$ with mean-squared amplitude normalization and f1–f5 one-sided power spectra of $\mathit{\Delta }{R}_b^{(off)}(t)[=R_b^{(off)}(t)-\overline{R_b^{(off)}(t)}]$ with mean-squared amplitude normalization. Each power spectrum is made of $2^{15}$ data points and it is smoothed by the Daniell filters of lengths 3 and 5. Plots of realistic frequency-domain bursting order parameters g1 ${⟨{\mathit{\beta }}_b^{on)}⟩}_r$ and g2 ${⟨{\mathit{\beta }}_b^{off)}⟩}_r$ versus $D$: ${⟨{\mathit{\beta }}_b^{(on)}⟩}_r$ and ${⟨{\mathit{\beta }}_b^{(off)}⟩}_r$ are obtained through average over 20 realizations for each $D$