Data-Driven Method to Estimate Nonlinear Chemical Equivalence

Abstract

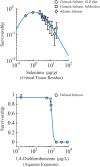
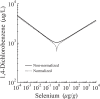
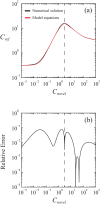
There is great need to express the impacts of chemicals found in the environment in terms of effects from alternative chemicals of interest. Methods currently employed in fields such as life-cycle assessment, risk assessment, mixtures toxicology, and pharmacology rely mostly on heuristic arguments to justify the use of linear relationships in the construction of "equivalency factors," which aim to model these concentration-concentration correlations. However, the use of linear models, even at low concentrations, oversimplifies the nonlinear nature of the concentration-response curve, therefore introducing error into calculations involving these factors. We address this problem by reporting a method to determine a concentration-concentration relationship between two chemicals based on the full extent of experimentally derived concentration-response curves. Although this method can be easily generalized, we develop and illustrate it from the perspective of toxicology, in which we provide equations relating the sigmoid and non-monotone, or "biphasic," responses typical of the field. The resulting concentration-concentration relationships are manifestly nonlinear for nearly any chemical level, even at the very low concentrations common to environmental measurements. We demonstrate the method using real-world examples of toxicological data which may exhibit sigmoid and biphasic mortality curves. Finally, we use our models to calculate equivalency factors, and show that traditional results are recovered only when the concentration-response curves are "parallel," which has been noted before, but we make formal here by providing mathematical conditions on the validity of this approach.

Fig 1. Illustration of the method used to determine chemical equivalence.

Concentration-response functions for two chemicals, termed “reference” (left panel) and “novel” (middle panel), can be used to parameterize the relationship between chemical concentrations (right panel).

Fig 2. Non-monotone, or “biphasic,” response function.

Positive (red line) and negative (blue line) affectors combine to result in a biphasic response function.

Fig 3. Survivorship data for Daphnia magna.

Experimental concentration-response data from [25] carried out on the water flea Daphnia magna, illustrating sigmoid survivorship curves. These data were fit to empirical sigmoid equations (solid and dotted lines).

Fig 4. Survivorship data for salmon and fathead minnow.

(Top panel) Experimental data illustrating a non-monotone survivorship curve for two species of salmon, Oncorhynchus tshawytscha and Salmo salar [30, 31], versus Se body-burden measured in μg Se per g dry wt tissue. (Bottom panel) A sigmoid survivorship concentration-response curve measuring a cumulative toxic effect for Fathead minnow (Pimephales promelas). Data obtained from [33].

Fig 5. Concentration-concentration relationships derived from sigmoid survivorship data.

Comparison between non-normalized (left panels) and normalized (right panels) concentration-concentration response functions derived from the sigmoid data of Fig 3.

Fig 6. Concentration-concentration relationships derived from sigmoid and biphasic survivorship data.

Comparison between non-normalized (solid line) and normalized (dotted line) sigmoid and biphasic concentration-response functions derived from the data of Fig 4.

Fig 7. Validity of the sigmoid and biphasic concentration-concentration relationships.

(a) Validity of the analytic equations for the concentration-concentration relationship (red line) given by Eqs 5–18 in the main text, overlaid with “exact” numerical results (black line). (b) Absolute value of the relative error between the analytic equations and the exact numerical result.