Nanodosimetry-Based Plan Optimization for Particle Therapy
- PMID: 26167202
- PMCID: PMC4475762
- DOI: 10.1155/2015/908971
Nanodosimetry-Based Plan Optimization for Particle Therapy
Abstract
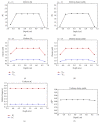
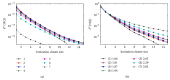
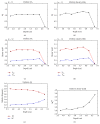
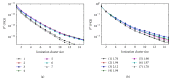
Treatment planning for particle therapy is currently an active field of research due uncertainty in how to modify physical dose in order to create a uniform biological dose response in the target. A novel treatment plan optimization strategy based on measurable nanodosimetric quantities rather than biophysical models is proposed in this work. Simplified proton and carbon treatment plans were simulated in a water phantom to investigate the optimization feasibility. Track structures of the mixed radiation field produced at different depths in the target volume were simulated with Geant4-DNA and nanodosimetric descriptors were calculated. The fluences of the treatment field pencil beams were optimized in order to create a mixed field with equal nanodosimetric descriptors at each of the multiple positions in spread-out particle Bragg peaks. For both proton and carbon ion plans, a uniform spatial distribution of nanodosimetric descriptors could be obtained by optimizing opposing-field but not single-field plans. The results obtained indicate that uniform nanodosimetrically weighted plans, which may also be radiobiologically uniform, can be obtained with this approach. Future investigations need to demonstrate that this approach is also feasible for more complicated beam arrangements and that it leads to biologically uniform response in tumor cells and tissues.
Figures
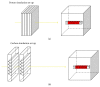
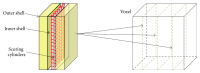
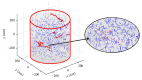
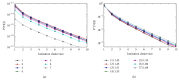



References
-
- Mihailescu D., Borcia C. Biophysical models in hadrontherapy. Journal of Advanced Research in Physics. 2012;3(1)011210
-
- International Atomic Energy Association (IAEA) IAEA. TECDOC-1560. Vienna, Austria: IAEA; 2007. Dose reporting in ion beam therapy.
-
- International Atomic Energy Association (IAEA) TRS-461. Vienna, Austria: International Atomic Energy Association (IAEA); 2008. Relative biological effectiveness in ion beam therapy.
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

