Scaling and optimal synergy: Two principles determining microbial growth in complex media
- PMID: 26172732
- PMCID: PMC6653625
- DOI: 10.1103/PhysRevE.91.062703
Scaling and optimal synergy: Two principles determining microbial growth in complex media
Abstract
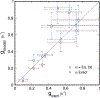
High-throughput experimental techniques and bioinformatics tools make it possible to obtain reconstructions of the metabolism of microbial species. Combined with mathematical frameworks such as flux balance analysis, which assumes that nutrients are used so as to maximize growth, these reconstructions enable us to predict microbial growth. Although such predictions are generally accurate, these approaches do not give insights on how different nutrients are used to produce growth, and thus are difficult to generalize to new media or to different organisms. Here, we propose a systems-level phenomenological model of metabolism inspired by the virial expansion. Our model predicts biomass production given the nutrient uptakes and a reduced set of parameters, which can be easily determined experimentally. To validate our model, we test it against in silico simulations and experimental measurements of growth, and find good agreement. From a biological point of view, our model uncovers the impact that individual nutrients and the synergistic interaction between nutrient pairs have on growth, and suggests that we can understand the growth maximization principle as the optimization of nutrient synergies.
Figures







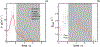
Similar articles
-
Phenomenological model for predicting the catabolic potential of an arbitrary nutrient.PLoS Comput Biol. 2012;8(11):e1002762. doi: 10.1371/journal.pcbi.1002762. Epub 2012 Nov 1. PLoS Comput Biol. 2012. PMID: 23133365 Free PMC article.
-
Optimal experimental design for discriminating between microbial growth models as function of suboptimal temperature.Math Biosci. 2014 Apr;250:69-80. doi: 10.1016/j.mbs.2014.01.006. Epub 2014 Jan 27. Math Biosci. 2014. PMID: 24480738
-
Modeling and optimization of hairy root growth in fed-batch process.Biotechnol Prog. 2010 May-Jun;26(3):847-56. doi: 10.1002/btpr.388. Biotechnol Prog. 2010. PMID: 20187141
-
Upflow anaerobic sludge blanket reactor--a review.Indian J Environ Health. 2001 Apr;43(2):1-82. Indian J Environ Health. 2001. PMID: 12397675 Review.
-
Comparing methods for metabolic network analysis and an application to metabolic engineering.Gene. 2013 May 25;521(1):1-14. doi: 10.1016/j.gene.2013.03.017. Epub 2013 Mar 26. Gene. 2013. PMID: 23537990 Review.
References
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
