Genetic variance components and heritability of multiallelic heterozygosity under inbreeding
- PMID: 26174022
- PMCID: PMC4675868
- DOI: 10.1038/hdy.2015.59
Genetic variance components and heritability of multiallelic heterozygosity under inbreeding
Abstract
The maintenance of genetic diversity in fitness-related traits remains a central topic in evolutionary biology, for example, in the context of sexual selection for genetic benefits. Among the solutions that have been proposed is directional sexual selection for heterozygosity. The importance of such selection is highly debated. However, a critical evaluation requires knowledge of the heritability of heterozygosity, a quantity that is rarely estimated in this context, and often assumed to be zero. This is at least partly the result of the lack of a general framework that allows for its quantitative prediction in small and inbred populations, which are the focus of most empirical studies. Moreover, while current predictors are applicable only to biallelic loci, fitness-relevant loci are often multiallelic, as are the neutral markers typically used to estimate genome-wide heterozygosity. To this end, we first review previous, but little-known, work showing that under most circumstances, heterozygosity at biallelic loci and in the absence of inbreeding is heritable. We then derive the heritability of heterozygosity and the underlying variances for multiple alleles and any inbreeding level. We also show that heterozygosity at multiallelic loci can be highly heritable when allele frequencies are unequal, and that this heritability is reduced by inbreeding. Our quantitative genetic framework can provide new insights into the evolutionary dynamics of heterozygosity in inbred and outbred populations.
Figures


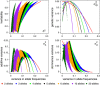
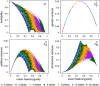
 (which is at p≈0.146 and ≈0.854), whereas heritability approaches maximal values at highly unequal allele frequencies.
(which is at p≈0.146 and ≈0.854), whereas heritability approaches maximal values at highly unequal allele frequencies.

Similar articles
-
Heterozygosity at a single locus explains a large proportion of variation in two fitness-related traits in great tits: a general or a local effect?J Evol Biol. 2014 Dec;27(12):2807-19. doi: 10.1111/jeb.12539. Epub 2014 Nov 23. J Evol Biol. 2014. PMID: 25370831
-
Genotypic selection in Daphnia populations consisting of inbred sibships.J Evol Biol. 2007 May;20(3):881-91. doi: 10.1111/j.1420-9101.2007.01313.x. J Evol Biol. 2007. PMID: 17465899
-
Population demography and heterozygosity-fitness correlations in natural guppy populations: An examination using sexually selected fitness traits.Mol Ecol. 2017 Sep;26(18):4631-4643. doi: 10.1111/mec.14243. Epub 2017 Aug 14. Mol Ecol. 2017. PMID: 28734054
-
Resolving the paradox of common, harmful, heritable mental disorders: which evolutionary genetic models work best?Behav Brain Sci. 2006 Aug;29(4):385-404; discussion 405-52. doi: 10.1017/S0140525X06009095. Behav Brain Sci. 2006. PMID: 17094843 Review.
-
On the correlation between heterozygosity and fitness in natural populations.Mol Ecol. 2002 Dec;11(12):2467-74. doi: 10.1046/j.1365-294x.2002.01644.x. Mol Ecol. 2002. PMID: 12453232 Review.
Cited by
-
Feed-backs among inbreeding, inbreeding depression in sperm traits, and sperm competition can drive evolution of costly polyandry.Evolution. 2017 Dec;71(12):2786-2802. doi: 10.1111/evo.13363. Epub 2017 Nov 13. Evolution. 2017. PMID: 28895138 Free PMC article.
-
Drivers of sex ratio bias in the eastern bongo: lower inbreeding increases the probability of being born male.Proc Biol Sci. 2019 May 15;286(1902):20190345. doi: 10.1098/rspb.2019.0345. Proc Biol Sci. 2019. PMID: 31064305 Free PMC article.
-
A father effect explains sex-ratio bias.Proc Biol Sci. 2017 Aug 30;284(1861):20171159. doi: 10.1098/rspb.2017.1159. Proc Biol Sci. 2017. PMID: 28855362 Free PMC article.
-
Application of single step genomic BLUP under different uncertain paternity scenarios using simulated data.PLoS One. 2017 Sep 28;12(9):e0181752. doi: 10.1371/journal.pone.0181752. eCollection 2017. PLoS One. 2017. PMID: 28957330 Free PMC article.
-
'Out of tune': consequences of inbreeding on bird song.Proc Biol Sci. 2016 Jul 27;283(1835):20161142. doi: 10.1098/rspb.2016.1142. Proc Biol Sci. 2016. PMID: 27466453 Free PMC article.
References
-
- Aparicio JM. (2011). The paradox of the resolution of the lek paradox based on mate choice for heterozygosity. Anim Behav 81: 1271–1279.
-
- Aparicio JM, Ortego J, Cordero PJ. (2006). What should we weigh to estimate heterozygosity, alleles or loci? Mol Ecol 15: 4659–4665. - PubMed
-
- Bolker BM. (2008) Ecological Models and Data in R. Princeton University Press: Princeton, NJ, USA.
-
- Borgia G. (1979) Sexual selection and the evolution of mating systems. In: Blum MS, Blum NA (eds). Sexual Selection and Reproductive Competition in Insects. Academic Press: New York, NY, USA.
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Other Literature Sources
Molecular Biology Databases

