Information Flow Between Resting-State Networks

Abstract

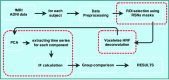
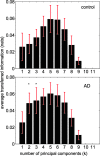
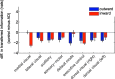
The resting brain dynamics self-organize into a finite number of correlated patterns known as resting-state networks (RSNs). It is well known that techniques such as independent component analysis can separate the brain activity at rest to provide such RSNs, but the specific pattern of interaction between RSNs is not yet fully understood. To this aim, we propose here a novel method to compute the information flow (IF) between different RSNs from resting-state magnetic resonance imaging. After hemodynamic response function blind deconvolution of all voxel signals, and under the hypothesis that RSNs define regions of interest, our method first uses principal component analysis to reduce dimensionality in each RSN to next compute IF (estimated here in terms of transfer entropy) between the different RSNs by systematically increasing k (the number of principal components used in the calculation). When k=1, this method is equivalent to computing IF using the average of all voxel activities in each RSN. For k≥1, our method calculates the k multivariate IF between the different RSNs. We find that the average IF among RSNs is dimension dependent, increasing from k=1 (i.e., the average voxel activity) up to a maximum occurring at k=5 and to finally decay to zero for k≥10. This suggests that a small number of components (close to five) is sufficient to describe the IF pattern between RSNs. Our method--addressing differences in IF between RSNs for any generic data--can be used for group comparison in health or disease. To illustrate this, we have calculated the inter-RSN IF in a data set of Alzheimer's disease (AD) to find that the most significant differences between AD and controls occurred for k=2, in addition to AD showing increased IF w.r.t.

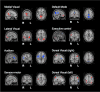
Controls: The spatial localization of the k=2 component, within RSNs, allows the characterization of IF differences between AD and controls.

Keywords: Alzheimer's disease; functional magnetic resonance imaging; independent component analysis; multivariate Granger causality; resting state networks.

FIG. 1.

Methodological sketch. Red (dashed) rectangles indicate key stages in our approach. Color images available online at www.liebertpub.com/brain

FIG. 2.

Average transferred information between all resting-state networks (RSNs) as a function of the number of principal components. Control (top) versus Alzheimer's disease (AD; bottom). The pattern of transferred information is the same for the two conditions; it increases from k=1 up to the maximum at k=5 to start to decrease up to zero information for k≥10. This means that the k=5 multivariate information flow (IF) between the different RSNs is most informative than in any other dimension. * Represents statistical differences between control and AD, p=0.05 (Bonferroni correction). Standard error (depicted in red) has been calculated across subjects for each group, control (n=10) versus AD (n=10). Information has been calculated in nats (i.e., Shannon entropies have been calculated in natural logarithms); however, to transform to information bits, we have to multiply the value in nats by 1.44. Color images available online at www.liebertpub.com/brain

FIG. 3.

Networks of IF between the different RSNs. For k=2 (occurring as the biggest difference between control and AD in Fig. 2), we have represented the multivariate IF between the different RSNs. Control (left) versus AD (right) for the two directions of IF (top and bottom). IF values are proportional to arrow thickness. Values represented in Figure 2 are the average among all the arrows represented in this figure, taking into account the two flow directions (top and bottom). Only for visualization purposes, values of IF have been normalized to the common maximum (marked with the red arrow), corresponding to transfer entropy (TE)=0.078 nats from the executive control network to the medial visual (left) in the AD condition. Dashed arrow from the sensorimotor network to the medial visual corresponds to the minimum value, which before normalization was TE=0.006 and after normalization was fixed to zero. Color images available online at www.liebertpub.com/brain

FIG. 4.

Control minus AD differences in the total IF per RSN. Outward information (blue) and inward information (red) from/to each different RSN. Error bars have been calculated across subjects for each group. Notice that values in this figure are much higher than those in Figure 2 due to two reasons: first, values in Figure 2 correspond to the average value of IF, taking off principal diagonal elements, this implied dividing each IF value by a factor of 56. Second, because to calculate both outward and inward information, we sum over columns and rows, respectively, and this meant multiplying each IF value by a factor of 6 (not including the self-node information and the element in the principal diagonal). Thus, values in this figure might be even up to 336 times bigger. Color images available online at www.liebertpub.com/brain

FIG. 5.

Brain maps of statistical significance localizing the k=2 component within each RSN. After a two-sample unpaired t-test (see the Materials and Methods section), we are representing two possible contrasts: in red, the figure shows the significant activity existing in AD, but nonexistent in control. In blue, vice versa, differences, which exist in control, but not in AD. Color images available online at www.liebertpub.com/brain