Overfitting Bayesian Mixture Models with an Unknown Number of Components

Abstract

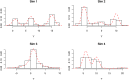
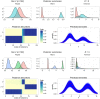
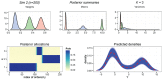
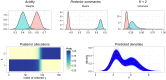
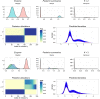
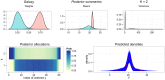
This paper proposes solutions to three issues pertaining to the estimation of finite mixture models with an unknown number of components: the non-identifiability induced by overfitting the number of components, the mixing limitations of standard Markov Chain Monte Carlo (MCMC) sampling techniques, and the related label switching problem. An overfitting approach is used to estimate the number of components in a finite mixture model via a Zmix algorithm. Zmix provides a bridge between multidimensional samplers and test based estimation methods, whereby priors are chosen to encourage extra groups to have weights approaching zero. MCMC sampling is made possible by the implementation of prior parallel tempering, an extension of parallel tempering. Zmix can accurately estimate the number of components, posterior parameter estimates and allocation probabilities given a sufficiently large sample size. The results will reflect uncertainty in the final model and will report the range of possible candidate models and their respective estimated probabilities from a single run. Label switching is resolved with a computationally light-weight method, Zswitch, developed for overfitted mixtures by exploiting the intuitiveness of allocation-based relabelling algorithms and the precision of label-invariant loss functions. Four simulation studies are included to illustrate Zmix and Zswitch, as well as three case studies from the literature. All methods are available as part of the R package Zmix, which can currently be applied to univariate Gaussian mixture models.

Fig 1. Description of the four simulations considered in this paper.

Density plots of the mixture distributions are indicated by a dashed line, and histograms of a single realisation of each simulation (with n = 200) are included.

Fig 2. Number of alive (non-empty) groups K¯0j for each chain j for Sim 2.

Results are shown for Sim 2, n = 100 (left) and n = 200 (right). Boxplots of the number of non-empty groups ${\underset{¯}{K}}_0^j$ for each chain j are included; each chain represents posterior samples from the Zmix sampler with the hyperparameter α ^j on the mixture weights, the value of which is included in red for each j.

Fig 3. Sim 2, n = 200, 𝓚_k0 = 3.

Results of Zmix and Zswitch including, from top left to right: the posterior parameter densities of all parameters from estimated groups, the posterior probability of allocations for each observation for each component, and a density plot of the data over the densities of 10,000 predicted datasets of the same size from the posterior.

Fig 4. Summary of the results for Sim 2 and n = 100.

The first two rows of plots refer to 𝓚_k0 = 2, and the lower set refers to 𝓚_k0 = 3. Results of Zmix and Zswitch are presented including, from upper left to lower right of each set: the posterior parameter densities of all parameters from estimated groups, the posterior probability of allocations for each observation for each component, and a density plot of the data over the densities of 10,000 predicted datasets of the same size from the posterior. A panel of plots is included for each candidate model found by Zmix.

Fig 5. Overfitting the Acidity dataset.

Results of Zmix and Zswitch including from upper left to lower right: the posterior parameter densities of all parameters from estimated groups, the posterior probability of allocations for each observation for each component, and a density plot of the data over the densities of 10,000 predicted datasets of the same size from the posterior.

Fig 6. Overfitting the Enzyme dataset.

Results of Zmix and Zswitch including, from upper left to lower right: the posterior parameter densities of all parameters from estimated groups, the posterior probability of allocations for each observation for each component, and a posterior predictive density plot of 10,000 replicates with the density of the data represented as a dashed line.

Fig 7. Overfitting the Galaxy dataset.

Results of Zmix and Zswitch including, from top left to right: the posterior parameter densities of all parameters from estimated groups, the posterior probability of allocations for each observation for each component, and a density plot of the data overlaid over the densities of 10,000 predicted datasets of the same size from the posterior.