Conditional Self-Entropy and Conditional Joint Transfer Entropy in Heart Period Variability during Graded Postural Challenge

Abstract

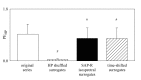
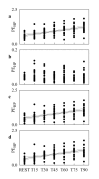
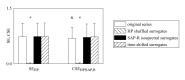
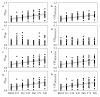
Self-entropy (SE) and transfer entropy (TE) are widely utilized in biomedical signal processing to assess the information stored into a system and transferred from a source to a destination respectively. The study proposes a more specific definition of the SE, namely the conditional SE (CSE), and a more flexible definition of the TE based on joint TE (JTE), namely the conditional JTE (CJTE), for the analysis of information dynamics in multivariate time series. In a protocol evoking a gradual sympathetic activation and vagal withdrawal proportional to the magnitude of the orthostatic stimulus, such as the graded head-up tilt, we extracted the beat-to-beat spontaneous variability of heart period (HP), systolic arterial pressure (SAP) and respiratory activity (R) in 19 healthy subjects and we computed SE of HP, CSE of HP given SAP and R, JTE from SAP and R to HP, CJTE from SAP and R to HP given SAP and CJTE from SAP and R to HP given R. CSE of HP given SAP and R was significantly smaller than SE of HP and increased progressively with the amplitude of the stimulus, thus suggesting that dynamics internal to HP and unrelated to SAP and R, possibly linked to sympathetic activation evoked by head-up tilt, might play a role during the orthostatic challenge. While JTE from SAP and R to HP was independent of tilt table angle, CJTE from SAP and R to HP given R and from SAP and R to HP given SAP showed opposite trends with tilt table inclination, thus suggesting that the importance of the cardiac baroreflex increases and the relevance of the cardiopulmonary pathway decreases during head-up tilt. The study demonstrates the high specificity of CSE and the high flexibility of CJTE over real data and proves that they are particularly helpful in disentangling physiological mechanisms and in assessing their different contributions to the overall cardiovascular regulation.

Fig 1. Graphical Representation of the Information-Theoretic Quantities in Ω = {y,x ₁,x₂}.

A mnemonic Venn diagram of the prominent information-theoretic quantities that are computed in the context of this study. The diagram is devised to represent in the information domain the dependency of the uncertainty associated to the current value of y = {y(n), n = 1002C…, N} quantified by the Shannon entropy (ShE) of y (ShE_y) on the information associated to past values of the assigned effect series y ^- = {[y(n-1), …, y(n-p)], n = p+1, …,N} quantified by ${\text{ShE}}_{y^{-}}$, and of two presumed causes x ₁ ^- = {[x ₁ (n-τ ₁),…, x ₁ (n-τ ₁-p)], n = τ ₁+p+1, …,N} and x ₂ ^- = {[x ₂ (n-τ ₂),…, x ₂ (n-τ ₂-p)], n = τ ₂+p+1, …,N} quantified by ${\text{ShE}}_{{\text{x}}_1^{-}}$ and ${\text{ShE}}_{{\text{x}}_2^{-}}$ respectively. The four intersecting circles (or ellipses) represent ShE_y, ${\text{ShE}}_{y^{-}}$, ${\text{ShE}}_{{\text{x}}_1^{-}}$ and ${\text{ShE}}_{{\text{x}}_2^{-}}$ (a). Notable quantities for this contribution are highlighted by filling in black the relevant areas at the interception of the circles (or ellipses): ShE_y (b), PE_y (c), SE_y (d), ${\text{CSE}}_{y|x_1,x_2}$ (e), ${\text{JTE}}_{x_1,x_2\to y}$ (f), ${\text{CJTE}}_{x_1,x_2\to y|x_1}$ (g), ${\text{CJTE}}_{x_1,x_2\to y|x_2}$ (h), and SE_y-${\text{CSE}}_{y|x_1,x_2}$ (i).

Fig 2. PE_HP Derived from Original Data and Surrogates.

Bar graph compares PE_HP computed during graded head-up tilt protocol over the original data (white bar), HP shuffled surrogates (backslash pattern bar), SAP-R isospectral surrogates (black bar) and time-shifted surrogates (slash pattern bar). The values are pooled together independently of the tilt table inclination and reported as mean plus standard deviation. The symbol # indicates a significant difference between original and surrogate series.

Fig 3. PE_HP during Graded Head-up Tilt.

Individual values (solid circles) of PE_HP as a function of the tilt table inclination computed over the original data (a), HP shuffled surrogates (b), SAP-R isospectral surrogates (c) and time-shifted surrogates (d). When the slope of the regression line is significantly larger then 0, the linear regression (solid line) and its 95 percent confidence interval (dotted lines) are plotted as well. A significant positive correlation on tilt table angles is found over the original data (a), SAP-R isospectral surrogates (c) and time-shifted surrogates (d).

Fig 4. Comparison between SE_HP and CSE_HP|SAP,R.

Grouped bar graph compares SE_HP and CSE_HP|SAP,R computed during graded head-up tilt protocol over the original data (white bars), HP shuffled surrogates (backslash pattern bars), SAP-R isospectral surrogates (black bars), and time-shifted surrogates (slash pattern bars). The values are pooled together independently of the tilt table inclination and reported as mean plus standard deviation. Within the same index (i.e. SE_HP or CSE_HP|SAP,R) the symbol # indicate a significant difference between original and surrogate series. Within the original data the symbol & indicates a significant difference between SE_HP and CSE_HP|SAP,R.

Fig 5. SE_HP and CSE_HP|SAP,R during Graded Head-up Tilt.

Individual values (solid circles) of SE_HP and CSE_HP|SAP,R as a function of the tilt table inclination computed over the original data (a,b), HP shuffled surrogates (c,d), SAP-R isospectral surrogates (e,f) and time-shifted surrogates (g,h). When the slope of the regression line is significantly larger then 0, the linear regression (solid line) and its 95 percent confidence interval (dotted lines) are plotted as well. A significant positive correlation on tilt table angles is found over the original data (a,b), SAP-R isospectral surrogates (e,f) and time-shifted surrogates (g,h) in the case of both SE_HP and CSE_HP|SAP,R.

Fig 6. Comparison between JTE_SAP,R→HP, CJTE_{SAP,R→HP|SAP} and CJTE_SAP,R→HP|R.

Grouped bar graph compares JTE_SAP,R→HP, CJTE_{SAP,R→HP|SAP} and CJTE_SAP,R→HP|R computed during graded head-up tilt protocol over the original data (white bars), HP shuffled surrogates (backslash pattern bars), SAP-R isospectral surrogates (back bars) and time-shifted surrogates (slash bars). The values are pooled together independently of the tilt table inclination and reported as mean plus standard deviation. Within the same index (i.e. JTE_SAP,R→HP, CJTE_{SAP,R→HP|SAP} or CJTE_SAP,R→HP|R) the symbol # indicates a significant difference between original and surrogate series. Within the original data the symbols & and § indicate a significant difference versus JTE_SAP,R→HP and CJTE_{SAP,R→HP|SAP} respectively.

Fig 7. JTE_SAP,R→HP, CJTE_{SAP,R→HP|SAP} and CJTE_SAP,R→HP|R during Graded Head-up Tilt.

Individual values (solid circles) of JTE_SAP,R→HP, CJTE_{SAP,R→HP|SAP} and CJTE_SAP,R→HP|R as a function of the tilt table inclination computed over the original data (a-c), HP shuffled surrogates (d-f), SAP-R isospectral surrogates (g-i) and time-shifted surrogates (j-l). When the slope of the regression line is significantly larger then 0, the linear regression (solid line) and its 95 percent confidence interval (dotted lines) are plotted as well. A significant positive correlation on tilt table angles is found only over the original data in the case of CJTE_{SAP,R→HP|SAP} (b) and CJTE_SAP,R→HP|R (c).