Ligand-induced changes of the apparent transition-state position in mechanical protein unfolding
- PMID: 26200872
- PMCID: PMC4621620
- DOI: 10.1016/j.bpj.2015.06.009
Ligand-induced changes of the apparent transition-state position in mechanical protein unfolding
Abstract
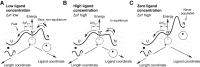
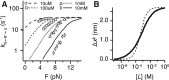
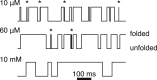
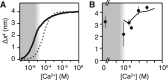
Force-spectroscopic measurements of ligand-receptor systems and the unfolding/folding of nucleic acids or proteins reveal information on the underlying energy landscape along the pulling coordinate. The slope Δx(‡) of the force-dependent unfolding/unbinding rates is interpreted as the distance from the folded/bound state to the transition state for unfolding/unbinding and, hence, often related to the mechanical compliance of the sample molecule. Here we show that in ligand-binding proteins, the experimentally inferred Δx(‡) can depend on the ligand concentration, unrelated to changes in mechanical compliance. We describe the effect in single-molecule, force-spectroscopy experiments of the calcium-binding protein calmodulin and explain it in a simple model where mechanical unfolding and ligand binding occur on orthogonal reaction coordinates. This model predicts changes in the experimentally inferred Δx(‡), depending on ligand concentration and the associated shift of the dominant barrier between the two reaction coordinates. We demonstrate quantitative agreement between experiments and simulations using a realistic six-state kinetic scheme using literature values for calcium-binding kinetics and affinities. Our results have important consequences for the interpretation of force-spectroscopic data of ligand-binding proteins.
Copyright © 2015 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Figures
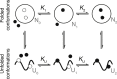



Similar articles
-
How do chemical denaturants affect the mechanical folding and unfolding of proteins?J Mol Biol. 2008 Jan 4;375(1):316-24. doi: 10.1016/j.jmb.2007.10.024. Epub 2007 Oct 15. J Mol Biol. 2008. PMID: 18021802
-
FEATHER: Automated Analysis of Force Spectroscopy Unbinding and Unfolding Data via a Bayesian Algorithm.Biophys J. 2018 Sep 4;115(5):757-762. doi: 10.1016/j.bpj.2018.07.031. Epub 2018 Aug 7. Biophys J. 2018. PMID: 30122292 Free PMC article.
-
Folding of horse cytochrome c in the reduced state.J Mol Biol. 2001 Oct 5;312(5):1135-60. doi: 10.1006/jmbi.2001.4993. J Mol Biol. 2001. PMID: 11580255
-
Force spectroscopy studies on protein-ligand interactions: a single protein mechanics perspective.FEBS Lett. 2014 Oct 1;588(19):3613-20. doi: 10.1016/j.febslet.2014.04.009. Epub 2014 Apr 18. FEBS Lett. 2014. PMID: 24747422 Review.
-
Coordinate and time-dependent diffusion dynamics in protein folding.Methods. 2010 Sep;52(1):91-8. doi: 10.1016/j.ymeth.2010.04.016. Epub 2010 May 11. Methods. 2010. PMID: 20438841 Review.
Cited by
-
Characterization of the interaction between the Sec61 translocon complex and ppαF using optical tweezers.Protein Sci. 2024 Jun;33(6):e4996. doi: 10.1002/pro.4996. Protein Sci. 2024. PMID: 38747383 Free PMC article.
-
Effects of Ligand Binding on the Energy Landscape of Acyl-CoA-Binding Protein.Biophys J. 2020 Nov 3;119(9):1821-1832. doi: 10.1016/j.bpj.2020.09.016. Epub 2020 Sep 24. Biophys J. 2020. PMID: 33080224 Free PMC article.
References
-
- Merkel R., Nassoy P., Evans E. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 1999;397:50–53. - PubMed
-
- Mossa, A., M. Manosas, …, F. Ritort. 2009. Dynamic force spectroscopy of DNA hairpins: I. Force kinetics and free energy landscapes. arXiv cond-mat.stat-mech. http://dx.doi.org/10.1088/1742-5468/2009/02/P02060. - DOI
-
- Rief M., Gautel M., Gaub H.E. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 1997;276:1109–1112. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
Other Literature Sources

