Stabilizing the central part of tropomyosin increases the bending stiffness of the thin filament

Abstract

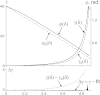
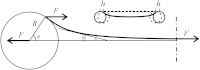
A two-beam optical trap was used to measure the bending stiffness of F-actin and reconstructed thin filaments. A dumbbell was formed by a filament segment attached to two beads that were held in the two optical traps. One trap was static and held a bead used as a force transducer, whereas an acoustooptical deflector moved the beam holding the second bead, causing stretch of the dumbbell. The distance between the beads was measured using image analysis of micrographs. An exact solution to the problem of bending of an elastic filament attached to two beads and subjected to a stretch was used for data analysis. Substitution of noncanonical residues in the central part of tropomyosin with canonical ones, G126R and D137L, and especially their combination, caused an increase in the bending stiffness of the thin filaments. The data confirm that the effect of these mutations on the regulation of actin-myosin interactions may be caused by an increase in tropomyosin stiffness.

Figure 4

The theoretical dependence of the dimensionless force, γ, and angle, φ, on the dimensionless bead displacement, δ, obtained by computer calculations using the theory developed here are shown by continuous lines. The same dependencies calculated with the theory of Dupuis et al. (12) are denoted with subscript index D and shown by dashed lines. The difference, Δγ, between the computer calculated γ value and its approximation is shown in the bottom plot by a continuous line. It is <0.12, i.e., lies within the precision of our experiments. Dotted line shows the difference between the two theories.

Figure 1

Strain-force diagram for a dumbbell containing reconstructed thin filaments containing the C190A Tpm. (A) The dependence of the pulling force on the dimensionless strain (squares), where h is the change in the half-distance between the beads, and R is the radius of the bead. Inset shows the micrographs of the beads for the first and the last data points before and at the end of the 12-step stretches. The positions of the centers of gravity of the bead images are shown by vertical lines. (B) One-dimensional profiles of the light intensity for the bead configurations shown in (A). The thresholds for determining the positions of the bead centers and the positions themselves are also indicated by horizontal and vertical lines, respectively.

Figure 2

Two beads of radii R held by optical traps are connected by an actin filament (bold line) to form a dumbbell as shown in the inset; the solid lines show the bead positions and the configuration of the filament under stretch of the dumbbell by a tensile force F. The unstrained positions of the beads and configuration of the filament are shown by the dashed lines. The middle of the filament is shown in the stretched and nonstretched dumbbell positions to symmetrize the picture. The left bead and a half of the filament are shown on an expanded scale; the symmetry plane is shown as a dot-dash vertical line on the right. The, stretching force, F, and the angle to the point of filament attachment on the bead, φ, are also shown.

Figure 3

Pooled data for the fitted strain-force diagrams obtained from several stretch cycles for at least three dumbbells (shown by different symbols) for F-actin (A) and reconstructed thin filaments containing either Tpm C190A (B) or Tpms G126R/C190A (C), D137L/C190A (D), and G126R/D137L/C190A (E). Continuous lines are the theoretical fitting curves calculated with Eq. 1 using optimized parameters K and δ₀, which provide the least mean-square deviation from the data points. Averaged traces for all panels (A–E) are presented in Fig. S1.