Single-trial dynamics of motor cortex and their applications to brain-machine interfaces
- PMID: 26220660
- PMCID: PMC4532790
- DOI: 10.1038/ncomms8759
Single-trial dynamics of motor cortex and their applications to brain-machine interfaces
Abstract
Increasing evidence suggests that neural population responses have their own internal drive, or dynamics, that describe how the neural population evolves through time. An important prediction of neural dynamical models is that previously observed neural activity is informative of noisy yet-to-be-observed activity on single-trials, and may thus have a denoising effect. To investigate this prediction, we built and characterized dynamical models of single-trial motor cortical activity. We find these models capture salient dynamical features of the neural population and are informative of future neural activity on single trials. To assess how neural dynamics may beneficially denoise single-trial neural activity, we incorporate neural dynamics into a brain-machine interface (BMI). In online experiments, we find that a neural dynamical BMI achieves substantially higher performance than its non-dynamical counterpart. These results provide evidence that neural dynamics beneficially inform the temporal evolution of neural activity on single trials and may directly impact the performance of BMIs.
Figures
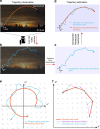
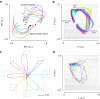
 . (b) The ratio of the (high-dimensional) neural population speed during the hold epoch to the reach epoch is 0.72 (blue), indicating that the rate of change of the neural population activity is less in the hold epoch than in the reach epoch. The dynamical model captures this feature, with the ratio of the neural state speed predicted by the model in the hold epoch to those in the reach epoch being 0.55 (purple). (c) Same as (b), but for Monkey L. The ratio of the high-dimensional neural velocities is 0.88; the ratio of the model-predicted neural state velocities is 0.79. (d) The averaged single-trial hand velocities during the hold and reach epochs are shown in grey. The average of the decoded single-trial velocities during the hold epoch are comparably low for both the high-dimensional neural data (yk, blue bar) and the dynamical neural state (sk, orange bar). However, during the reach epoch, the dynamical neural state is able to decode significantly higher velocities. (e) Same as (d) but for Monkey L.
. (b) The ratio of the (high-dimensional) neural population speed during the hold epoch to the reach epoch is 0.72 (blue), indicating that the rate of change of the neural population activity is less in the hold epoch than in the reach epoch. The dynamical model captures this feature, with the ratio of the neural state speed predicted by the model in the hold epoch to those in the reach epoch being 0.55 (purple). (c) Same as (b), but for Monkey L. The ratio of the high-dimensional neural velocities is 0.88; the ratio of the model-predicted neural state velocities is 0.79. (d) The averaged single-trial hand velocities during the hold and reach epochs are shown in grey. The average of the decoded single-trial velocities during the hold epoch are comparably low for both the high-dimensional neural data (yk, blue bar) and the dynamical neural state (sk, orange bar). However, during the reach epoch, the dynamical neural state is able to decode significantly higher velocities. (e) Same as (d) but for Monkey L.
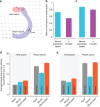
 . Most BMI systems decode using noisy neural observations, yk, which comprise the single-trial spike counts of the neural data. This data (smoothed) is shown for a single channel, where the light blue traces denote the single-trial neural observations when a monkey intended to reach downwards. The bolded trace is the firing rate averaged over trials (relative to the start of the trial), or peristimulus time histogram. To the right of the decoder block, the black traces denote the true path of the cursor for trials where the monkey reaches from the upper square target to the lower square target (where both squares are 4 × 4 cm). The bolded trajectory is the average path of the cursor across single-trials. The offline reconstructions using the dynamical neural state result in a superior offline decode when compared with using the the non-dynamical binned spike counts.
. Most BMI systems decode using noisy neural observations, yk, which comprise the single-trial spike counts of the neural data. This data (smoothed) is shown for a single channel, where the light blue traces denote the single-trial neural observations when a monkey intended to reach downwards. The bolded trace is the firing rate averaged over trials (relative to the start of the trial), or peristimulus time histogram. To the right of the decoder block, the black traces denote the true path of the cursor for trials where the monkey reaches from the upper square target to the lower square target (where both squares are 4 × 4 cm). The bolded trajectory is the average path of the cursor across single-trials. The offline reconstructions using the dynamical neural state result in a superior offline decode when compared with using the the non-dynamical binned spike counts.
References
-
- Shenoy K. V., Sahani M. & Churchland M. M. Cortical control of arm movements: a dynamical systems perspective. Annu. Rev. Neurosci. 36, 337–359 (2013) . - PubMed
-
- Briggman K. L. & Kristan W. B. Jr. Multifunctional pattern-generating circuits. Annu. Rev. Neurosci. 31, 271–294 (2008) . - PubMed
-
- Petreska B. et al.. Dynamical segmentation of single trials from population neural data. Adv. Neural Inf. Process Syst. 24, 756–764 (2011) .
-
- Rokni U. & Sompolinsky H. How the brain generates movement. Neural Comput. 24, 289–331 (2012) . - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

